【黎斯算子的分解】
拼译：the decomposition of Riesz operators
又称黎斯算子的韦斯特(West)分解。这是泛函分析方向算子理论中的一课题。
设X是一个复的无限维巴拿赫空间，B(X)、K(X)和Q(X)分别表示X上线性有界算子全体、紧算子全体和拟幂零算子全体。一个线性有界算子T被称为黎斯算子，是指T的谱具有和紧算子一样的谱结构：谱σ(T)是一个至多可数集，唯一可能的聚点是零，非零谱点都是T的孤立有限代数重特征值。黎斯算子的全体记为R(X)。由定义直接得到包含关系：R
和
。并且，由算子紧摄动理论知识有
。1966年，爱尔兰的韦斯特(T．T．West)证明：当X是希尔伯特空间H时，R(H)=K(H)+Q(H)。就是说，希尔伯特空间上的每一个黎斯算子T，可分解为一个紧算子K与一个拟幂零算子Q的和：T=K+Q。从此，对于一般巴拿赫空间X上的黎斯算子，是否也都可作这种所谓韦斯特分解的问题，就提了出来，引起算子理论界的兴趣和关注。1984年，《线性与复分析问题集》一书把它列为当代分析方向未解决的课题之一。该课题的研究与巴拿赫空间上算子紧摄动及算子理想等课题的研讨直接或间接地相联系。70年代和80年代前期，黎斯算子分解的研究进展甚微。有过一种猜测：在相差一个线性同胚的意义上说，只有希尔伯特空间，其上所有的黎斯算子可韦斯特分解。1980年，劳里(Laurie)和拉德佳维(Radjavi)得到过黎斯算子可West分解的一个充分条件：∑n｜λn｜＜∞(其中λn是T的非零特征值按各自的代数重数重复的一个排列)。后来，这一分解条件被减弱为：∑｜λn｜＜∞。另外，还讨论过黎斯算子带附加条件的韦斯特分解。例如，当黎斯算子T可韦斯特分解T=K+Q，而且KQ=QK时，称T具有完全的韦斯特分解；当分解式T=K+Q满足KQ－QK∈Q(X)时，称T具有次完全的韦斯特分解，等等。道松(H．R．Dowson)举例说明，即便是希尔伯特空间H，也存在黎斯算子T∈R(H)，T虽可韦斯特分解但不可完全分解。后来，史密斯(Smith)等人又证明：希尔伯特空间H上的每一个黎斯算子可有次完全的韦斯特分解。1986年，加拿大的戴维森(Davidson)与美国的埃雷罗(Herrero)合作，取得了课题研究的突破性进展，否定了“只有希尔伯特空间，其上所有的黎斯算子可韦斯特分解”的猜测。他们证明，如果巴拿赫空间X具有有限维P块分解结构，则X上的每个黎斯算子都可韦斯特分解。因而获知一大类非希尔伯特空间，包括经典序外空间co，lp(1≤p＜∞)在内，其上的每个黎斯算子都可韦斯特分解。这一进展是采用构造紧摄动算子K的新方法取得的。以往的方法，限于构造主对角线元素依次为T的非零特征值的上三角矩阵型式的紧摄动算子K。简单地说，K的型式为T的“原有型式”所限，如图所示：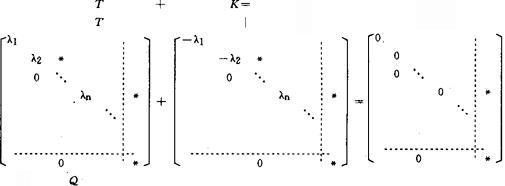
而戴维森和埃雷罗的方法是：先构造一个T的紧摄动算子K1，使得T+K1，有一个无限维零空间Ker(T+K1)。然后，根据具体需要，让Ker(T+K1)依次作适当的有限维方块，分别和T+K1的各特征子空间穿插结合成块上三角矩阵型式。如下图示，“改造”后的T+K1形如：
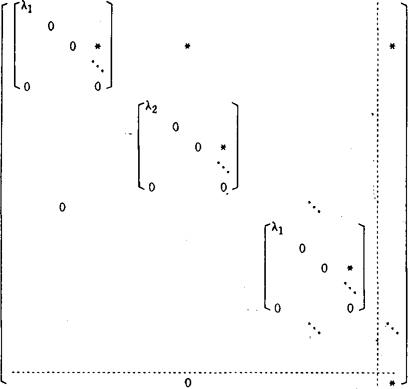
然后，在T+K1的每一“主对角”块元素的相应位置，构造紧算子K2的“主对角块”，使得相应两“主对角块”之和是幂零算子。
1988年，钟怀杰改进和推广了上述新方法，证明包括函数空间Lp(μ)(1＜p＜∞)在内的更大一类巴拿赫空间上的黎斯算子也都可韦斯特分解。上述方法的第1个步骤，由于零属于黎斯算子T的左本性谱与右本性谱的交集，总可以构造第1个紧算子K1，使得Ker(T+K1)是无限维闭子空间，故对一般巴拿赫空间都可行。但第2个步骤，为了要构造第2个紧算子K2，要先在子空间Ker(T+K1)中取得一个与co或lp(1≤p＜∞)同构且在X中可补的无限维闭子空间，就存在作一般性推广的困难：并非每个巴拿赫空间含有与经典序列空间同构的可补子空间。最近，钟怀杰把巴拿赫空间局部理论研究成果应用到这一课题的研讨中，避免了获取无限维可补子空间的步骤，证明每一B－凸空间，其上所有的黎斯算子也可韦斯特分解，把研究朝问题肯定回答方面又推进了一步。新结果的意义在于：已知每个巴拿赫空间X，都具有介于数1和2之间的某一“型参数”p(X)(1≤p(X)≤2)，又知空间X具有B－凸性等价于X具有“型参数”P(X)＞1。那么，新结果使问题归结于在型参数P(X)=1的一类空间中研讨了。应用和改进已有的各种方法，预期还可在一些子空间结构性质较为清晰的巴拿赫空间，获得进一步肯定结果。近年来，国际上空间理论，尤其是局部理论研究日益深入，构造了一些性质“异常”的巴拿赫空间。这些空间为本课题的深入提供了远远超出经典巴拿赫空间范围的讨论对象。因而不应排除这种猜测：存在一个巴拿赫空间X，有黎斯算子T∈R(X)不可韦斯特分解。课题的深入，似乎更多地依赖于空间结构理论的进展。【参考文献】：1 West T T. The decomposition of Riesz operators, Proc London Math Soc,1966,16(3) :737～7522 Chui-Smith,Proc Amer Math Soc,1976,603 Dowson H R. London Math Soc monograph, 1978,124 Laurie C, et al. Bull London Math Soc 1980,12:130～1325 Lecture Notes in Math. Spinger Verlag,1984,10436 Davidson K R, et al. Indiana Univ Math J, 1986,35:333～ 3437 钟怀杰．科学通报，1988，7∶614～6158 钟怀杰．数学年刊，1990，11A(6)∶699～706(福建师范大学钟怀杰副教授撰；林辰审)