【教育系统工程】
拼译:educational systems engineering
即系统工程应用于教育系统的组织管理和运行。教育系统可分成宏观和微观两个范畴。微观是指一个教育单位,如一所学校。宏观是指国家、地区内的教育单位所组成的系统。教育系统工程运用数学模型的方法,进行定量分析,提出总体优化的方案和建议。教育系统工程的内容,就宏观来说,主要是人才的预测和规划。人才开发与社会经济、科学技术和教育事业的发展有着错综复杂的联系,存在着相互消长的辩证关系。社会的发展需要多种专业和多种层次的人才,必须保持合理的人才结构,才能充分发挥人才群体效益及各种层次人才的作用。为了做好人才规划,需要进行人才需求预测和人才拥有量分析。首先要调查研究现有专门人才的实际拥有量,分析现有在职专门人才的流动过程和转移规律,并在有关退休、晋升、调离等政策的基础上预测未来专门人才的拥有量。同时,可以在对事业发展预测的前提下,预测未来各种专业门类和各种学历层次的专门人才的需求量。
人才需求预测常用的方法有:(1)通过对历史资料进行统计,找出各类人才的需求量占职工总数的比例,再根据各个部门生产增长的幅度,利用回归分析等方法来预测职工总数的增长,例如: Y(t)=a0+d(t)x1(t)+β(t)x2(t)+γ(t)x3(t)式中y(t)为第t年的人才需求量,x1(t),x2(t),x3(t)分别是第t年的职工总数、人均占有固定资产、固定资产浮值,α(t),β(t),γ(t)分别是随时间变化的系数,α0是常数。
(2)利用计量经济模型进行预测。例如根据柯布-道格拉斯生产的函数,假定生产水平取决于劳动力和资本输入水平。则
式中P1是产出,C表示综合技术水平,M1,K1分别为测算期t内所使用的劳动力总数和资本总量,U1是随机干扰产生的误差,α和β是反映劳动力和资本产出和弹性数。对上式取对数,经过整理,可得到人才需求预测模型为:
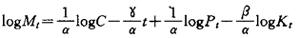
式中Mt,Pt和Kt为相应的估计值。
人才拥有量分析,既要预测在不同改革条件下各种专业、学历、职务、年龄的实际人才拥有量,又要预测逐年退休、死亡、调离、晋升、补充的实际人才数,详细揭示影响人才流动的各种因素和不同政策所造成的具体影响,以适应不同领导部门的决策需要。人才拥有量预测模型既要能反映人才变化的动态过程,又能从稳态角度反映人才的实际分布状况。一般可用马尔柯夫模型、状态或优化模型来反映人才的拥有量。人才拥有量预测的马尔柯夫模型为 i,j=1,2.……,K;t=1,2,……
i,j=1,2.……,K;t=1,2,……式中ni(t)为时刻t时i类人数,Pji为从j类向i类转移的转移率,γi(t)为在时间(t-1,t)内i类所补充的人数,K为分类数。如果把上式变成向量形式,则为
N(t)=N(t-1)P+R(t) t=1,2,……式中N(t)=[n1(t),n2(t),……,nk(t)]为时刻t时人数的行向量;R(t)=[r1(t),r2(t),……rk(t)]为在(t-1,t)时间中补充人数的行向量;P为各类人员之间的转移矩阵:
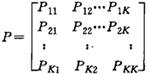
式中Xs(t)为学生年级向量
U(t+1)为(t+1)年入学和补充人数 As(t)为转移矩阵,描述t到t+1年度之间系统内部学生流动情况(如升级率、留级率、升学率等)(2)教师规划模型:教师需要量是根据学生状态向量及各学历层次的师生比进行计算的。 XO7(t)=GTS(t)·X5(t)式中XOT(t)为t年的教师需要量;GT5(t)为师生的转移矩阵;Xs(t)为t年的学生状态向量。
教师拥有量是考虑逐年教师的补充、调动、退休等情况而计算出的教师队伍的实际状态,可用如下状态方程来描述: XT(t+1)=AT(t)XT(t)+XTI(t+1)+WT(t+1)式中XT(t+1)为t+1年度的教师拥有量;XT(t)为t年度的教师状态向量;AT(t)为教师流动的教师转移矩阵;XTI(t+1)为t+1年度补充的教师数;WT(t+1)为各种意外扰动向量。
根据学生数量算出的教师需要量和根据教师状态方程算出的教师拥有量之间总是存在一定的差额。毕业生分配当教师的人数XTI(t+1)为决策变量。决策部门按差额来确定合理的分配方案,使需要量与拥有量之间保持平衡。应用教育经费预测子模型,可描述各类学校培养量和投资、经费的关系,预测出逐年的教育事业费、基建投资和总教育经费。将教育规划子模型与教育经费预测子模型配合,可分析教育投资和教育发展速度的定量关系。与此同时,中国各高等学校开始建立了计算机辅助管理系统,有些高校还开展了计算机辅助教学的应用研究【参考文献】:1 周具隆,周承业编著.专门人才需求预测方法.北京:高等教育出版社,19852 汪应洛,等.教育规划模型及其应用.北京:科学出版社,19883 朱佳生.教育系统工程.长沙:湖南大学出版社,1989(西安交通大学汪应洛教授撰)