【多轴非比例加载下低周疲劳寿命估测】
拼译：multiaxial low-cycle fatigue life under nonproportional loading
疲劳破坏通常是工程结构破坏的主要形式。疲劳问题受到多种因素的影响，如应力应变状态、环境、材料组织等，涉及到力学、材料学、物理学和化学等多学科，以往的研究主要集中于单轴状态下的疲劳问题。然而，工程中的结构元件如传动轴、涡轮机叶片、压力容器等一般承受的是双轴或三轴应力状态。由于单轴疲劳与多轴疲劳的破坏机制不尽相同，故在把单轴疲劳的研究成果推广到多轴疲劳时并不能得到满意的结果，特别是在非比例加载低周疲劳时，将给出不安全的预测，所以迫切需要对多轴非比例加载下的疲劳进行研究。随着新型多轴疲劳试验机的诞生，使得这一方面的研究可能进行。对多轴非比例循环加载下材料的循环本构行为研究表明，非比例循环加载下材料的本构行为与比例循环加载下有着本质差别。材料在非比例循环加载下存在明显的附加强化，其塑性流动特性以及应力、应变迟滞回线的形状与比例加载时均有较大差异。由于存在应力的附加强化，从而导致非比例循环加载下低周疲劳寿命大大减少。
低周疲劳寿命的研究，从50年代著名的曼森－科芬(Manson-Coffin)公式问世以来已近40年，而对于多轴低周疲劳的研究，特别是对于在多轴非比例循环加载下的低周疲劳研究只是近年才开展起来。所谓低周(应变)疲劳是指疲劳应力接近或超过材料的屈服极限，材料在每一个应力－应变循环中均有一定数量的塑性变形，其疲劳寿命比较短，一般低于105循环。1954年曼森(Manson)、科芬(Coffin)认为对于单轴拉压低周疲劳塑性应变的积累是其破坏的主要原因，因此，以塑性应变幅Δεp作为损伤参量进行疲劳寿命估算，可以较好地描述材料的低周疲劳行为。对于多轴低周疲劳破坏的损伤分析和寿命估算一般有3种方法：等效应变法、能量法和临界面法，但尚未形成一种对各种材料和载荷普适的理论，多为经验的或半经验的。1981年辛纳斯(Sines)等提出的等效应变法是将曼森－科芬(Mansin-Ciffin)公式推广用于多轴低周疲劳，其损伤参量为等效应变Δεeq，它可以是八面体剪应变，最大剪应变或冯·密塞斯(Von Mises)等效应变，这种等效应变往往是从强度理论引伸而来。能量法认为塑性形变功，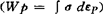
，的累积是产生材料不可逆损伤进而导致材料疲劳破坏的主要原因，将这一概念成功地用于单轴低周疲劳后，许多学者将其推广到多轴低周疲劳。1984年伊林(Ellyin)等采用密塞斯(Mises)等效应力、等效应变和幂律本构关系，以破坏时多轴塑性形变功累积与单轴塑性形变功累积等效得到多轴疲劳寿命判据。临界面法认为疲劳破坏由破坏面及关于这个面上的应力和应变状态来决定。首先计算疲劳临界面上的应力、应变，然后，将临界面位置的应力、应变历史转化成累积的疲劳损伤。1973年布朗(Brown)和米勒(Miller)提出了由最大剪应变面上的两个参量控制疲劳破坏，即最大剪应变γmax和所在面上的法向应变
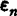。之后，不同学者选择了不同的临界面和损伤参量，对上法进行了修正。在非比例循环加载下(即不同方向的循环载荷呈非比例加载)的低周疲劳，因其应变主轴不断旋转，建立在等效应力、应变关系上的循环应力－应变关系不是唯一的，而取决于加载的非比例度。非比例循环加载将产生明显的附加强化，并且明显地影响疲劳寿命。1987年索西(Socie)对304不锈钢低周疲劳研究的结果表明，在圆形路径下，附加强化增加一倍，疲劳寿命减少90%；对In718合金，附加强化增加10%～15%，疲劳寿命减少50%。因此必须对非比例循环加载下的低周疲劳及损伤积累规律进行具体研究，否则将导致不安全的预测。1977年卡纳扎瓦(Kanazawa)等研究了拉扭组合的非比例循环加载下的低周疲劳，认为最大剪应变面(临界面)上的最大剪应变γmax和法向应变en控制疲劳损伤发展。研究表明，低周疲劳时，在相同等效应变幅值下的非比例加载比比例加载产生更多的损伤，90°相位差的非比例加载给出最短的疲劳寿命，而比例循环加载给出最长的疲劳寿命。他们还发现，等效应变法用于非比例循环加载条件下是偏于危险的。1980年雷斯(Leis)等对非比例循环加载进行的损伤分析，支持了Kanazawa的观点，但也指出采用纯应变进行损伤分析的不足。有些研究者从能量法的角度开展了这方面的研究。1981年伽德(Garud)用每循环塑性功拟合疲劳寿命，按增量塑性理论，引入莫鲁(Mroz)型强化律计算塑性功，处理比例加载和非比例加载疲劳。结果表明，预测偏于保守，误差达3倍，因此建议一个权因子作用在剪应变产生的塑性功上，文中取权因子为1／2。1987年索西(Socie)认为由于非比例循环加载下存在附加强化，致使疲劳寿命减少，故寿命估算中应考虑应力项。对In718合金的剪切型破坏采用计入最大剪应变面上的法向应力σno修正布朗(Brown)和米勒(Miller)的临界面法，给出了用于预测非比例循环加载下低周疲劳寿命的三参数判据。对于304不锈钢的拉伸型破坏，则在史密斯(Smith)等提出的判据中引入了最大主应变面的最大拉应力σ1max。1988年法梯密(Fatemi)和索西(Socie)在研究SAE1045钢时，对布朗和米勒(Brown and Miller)的临界面模型进行了另一种修正，即以临界面上的最大法向应力σnmax代替法向应变
。以上考虑应力修正的判据在实际应用时需要一个精细的本构关系计算应力。发展能描述材料非比例循环本构行为的本构方程，是近十年来国际上关于材料本构关系研究方面的一个热点，受到广泛的重视。尤其重要的是对材料在非比例循环加载下附加强化的描述，一种可行的方法是引入一个符合实际且具有一定物理基础的加载路径非比例度。巴纳拉(Benallal)和马丘斯(Marpuis)定义以应力或应变之间的夹角正弦为非比例度；伊林(Ellyin)和夏(Xia)定义塑性应变路径在π平面上的投影面积比值为非比例度；麦道威尔(Mcdowell)定义塑性应变在最大塑性应变幅的方向上的投影积分为非比例度等等。尽管这些定义都可以描述某些路径的强化行为，然而各有其局限性，特别对经过原点的直线段路径，如对十字形路径、射线状路径不能很好加以描述。因此，发展适当的非比例度定义对研究非比例循环本构关系和低周疲劳是至关重要的。1990年以来，在国家自然科学基金重大项目资助下，西南交通大学开展了关于多轴非比例加载低周疲劳研究。研究的重点为：(1)定义了一个具有物理基础、适用性广的加载路径非比例度，该参量是一个与单元体各个方向上最大剪应变分布有关的量，体现了非比例强化与材料剪切滑移的联系。(2)建立了一个简单的用非比例度修正的非比例循环本构关系。(3)基于连续损伤力学方法，在损伤演化方程中引入路径的非比例度，结合布朗(Brown)和米勒(Miller)的临界面模型，建立了一个新的非比例加载下低周疲劳损伤分析的临界面模型，给出了可用于非比例加载下低周疲劳寿命预测的Manson-Coffin型公式。对多轴非比例加载下的低周疲劳问题进行研究是十分复杂和困难的。如何从微观或细观层次对非比例强化以及疲劳损伤进行微观机制的观察、分析和研究，揭示疲劳破坏的本质，给出精确的循环本构关系和疲劳寿命预测，是今后这方面研究工作的重点。【参考文献】：1 Manson S S. Behavior of material under conditions of ther-mal stress, NACA report, 1954,11702 Coffin L F. Journal of Engineering Material and Technolo-gy, 1954,76:931～9503 Brown M W et al. Proc Inst Mech Engngrs, 1973,187:745 ～7554 Kanazawa K et al. Journal of Engineering Material and Technology, 1977,99:222～2285 Sines G et al. Journal of Engineering Material and Technol-ogy, 1981,103:82～906 Garud Y S. Journal of Engineering Materrial and Technology, 1981,103:118～1257 Ellyin F et al. Journal of Pressure Vessel and Technology, 1984,106:342～3478 Socie D F. Journal of Engineering Material and Technology, 1987,109:293～2989 Fatemi A et al. Fatigue of Engineering Material and Struc-ture, 1988,14:149～165(西南交通大学应用力学研究所博士生导师高庆、陈旭副教授撰；孙训方教授审)