“分形理论在土壤科学中的应用”的概念、定义、翻译、参考文献-科学参考

单词

分形理论在土壤科学中的应用

释义

【分形理论在土壤科学中的应用】

分形理论是由Benoit B．Mandelbrot在1975年正式提出与建立的一种探索复杂性的新的科学方法和理论。它从自然几何学入手，进而在近十几年来已推广到物理、化学、天文、地学、材料工程、计算机科学、生物、医学等领域，另在经济学、艺术学、社会科学等其它方面也展现了令人注目的应用前景。理论研究与实验表明，在越混乱、越无规则、越复杂的领域，分形理论越能显示其应用魅力。土壤科学研究的主要任务就是要探讨在环境(包括自然、人为因素)的变化和制约下，土壤的形成、发生与演化过程以及土壤的空间分布规律与动态变化。由于发生在土体内的物理、化学生物等各种过程相互影响、同时进行，再加上外部无究随机各种地质过程与现代人为措施的影响，导致形成了土壤这一形态上与演化过程上都十分复杂的自然体。正因为如此，加之受研究方法、手段的限制，更主要提传统研究思想的禁锢，缺乏带有指导性新的理论与思想体系的引入与提出，从而使到目前为止，没有能完全做到对土壤形态与性质的定量化描述，如土壤结构的描述等；至于对各种土壤过程的定量化描述与模拟，更是与人们所要求的相差甚远。把分形理论及其研究方法引入到土壤科学研究中，无疑也将会推动土壤形态、过程复杂性问题的解决，并在一定程度上使其定量化。

分形理论分形或分形几何学一词是Mandelbrot为描述具有自相似性自然碎片或不规则结构而提出的。Mandelbrot指出，自然界许多曲线和形态在一定尺度范围内具有分形的性质，例如海岸线、河流水系、裂缝、云的边缘线等，土壤中的例子如毛细管的通道、湿润峰等。一个分形物体最主要的特征是它的“不规则程度”与尺度的大小无关，即具有自相似性。先看两个具体的实例。

实例1：海岸的轮廓线。对于某一特定轮廓的海岸线，用较小的步长ε₁量测时，总长度为L₁，当用较大的步长ε₂量测时，总长度为L₂，其中：

　　　　　L₁=N₁ε₁　　　　(1)

　　　　　L₁=N₂ε₂　　　　(2)

式中：N₁、N₂为量测的步长数。

显然，L₁＞L₂，即采用的步长越短，量测得到的海岸线长度越大，可见测量步长的选择对测量结果影响很大。

实例2：Tyler和Whearcraft假设土壤是由大小不一的球形颗粒组成，某一个毛细管通首的长度h，在取不同的测量步长d时，可由(3)、(4)式给出：

　　　　　h1=N₁d₁　　　　(3)

　　　　　h2=N₂d₂　　　　(4)

那么，同样可以得到实例1的结论。

上述结论，与人们已有的常识相“违背“，那么，海岩线到底有多长?土壤中某一毛细管的长度又是多少?要对上述问题做出圆满回答，必须引入分形或分形数学的理论和方法。

在欧几里德几何学中，我们能很容易地测量出一条直线的长度L。如果测量单位为ε(ε＜L)，那么：

　　　　　L(ε)=Nε¹=常数　　　　(5)

式中N为需要覆盖直线的测量单位的数目，指数1即为直线的拓朴维数。

如果我们所测量的不是规则线段，等式(5)就不成立，即对于任意的ε，L(ε)不是常数。仿照式(5)，对于不规则的线段(如海岸线)业已证明下式成立，即；

　　　　　F=Ne^D=常数　　　　　　　(6)

式中F：与e无关的所测量出的线段长度。D：产生此线段为一恒定长度(F)的维数，即定义为此线段的分形维数，分形维数(简称分维数)D是分形理论中最核心的概念与内容，它是度量不规则物体或分形体最主要的指标。分维数D不同，物体的复杂程度或它的动态演化过程就不相同，一般说来D不是整数。

合并式(5)、(6)，可得出：

　　　　　L(ε)=Fε^1－D　　　　　(7)

式(7)为对一条分形线，一维拓朴维数和分形维数D相互转化的关系式。

很容易把上述原理推广到二维、三维甚至更高维的欧氏空间中，从而可利用分维数D对高维分形物体进行描述。一般来说，在二维空间研究分形体表面积，在三维空间中研究分形体体积等。从另一个角度，现已把研究对象从仅限于几何量如长度、面积、体积等推广到其它物理量如质量、密度、电荷分布、物质含量、某一状态因子等，从而大大拓宽了分形理论的研究与应用领域，这说明了把分形几何学视为“大自然的几何学”是毫不夸张的。

分形理论在土壤科学中的应用分开理论应用于土壤科学研究，现仅处于开始探索阶段，但它所表现出的应用面之宽，以及所取得的成果，说明分形理论可能成为解决土壤科学中复杂性问题的有力工具之一。

1．分形理论在土壤机械组成(粒级分布)中的应用。Turcotte(1986)研究表明：地质沉积物中颗粒大小的分布表现出分形行为，且下式成立，即

　　　　　NRρ=常数　　　　　(8)

式中R₁为第i级的颗粒半径；N为大于半径R₁的粒子的总数目；D为颗粒大小分布的分形维数。

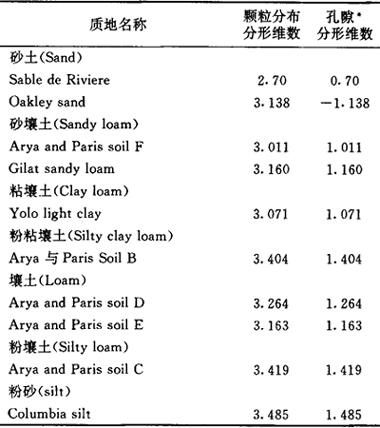
D反映了按大小颗粒的分布模式，当D=0时，土壤由单一直径的颗粒组成；当0＜D＜3．5时，土壤的机械组成中，大颗粒占优，当D＞3．0时，土壤的机械组成中小的颗粒(粉粒、粘粒)占优。Turcotte(1986)分析了21种土壤样品，D值都接近3．0。

根据(8)，应用土壤机械分析的数据，做出lnN～lnR₁关系曲线，即可确定出D．Tyler与Wheatcraft(1989)通过上述方法确定的D值见表1。

表1 根据颗粒大小分布数据所确定的分形维数

*利用式(24)计算得出。

2．土壤水分特征曲线的分形数学模型 Ayra和Parjs(1984)。利用土壤的粒级分布与容重数据，推导出了确定土壤水分特征曲线的机理--经验型模型。通过把颗粒贫布曲线分成n部分，对于单位质量的样品，每一部分所对应当量孔隙体积为：

那么相应的孔隙半径为：

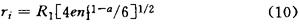
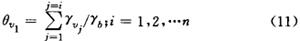
(9)、(10)式中γγ₁为孔隙体积，ω₁为固体质量，P_ρ为颗粒的比重，e为孔隙比，r_i为平均孔隙的半径；R₁为平均颗粒的半径；n₁为颗粒的数目；a为一经验常数，1．35≤a≤1．40。并假定孔隙全部为有效可充水孔隙。

根据(9)可求出θ_v1：

其中

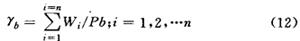
计算时，可取：=(θ_v1+θ_i+1) (13)

式中，γ_b：每单位土样的体积：

ρ_b：土壤容重。

根据(10)式，假定毛管为圆柱形，可求出ψ_i：

ψ_i=2γcosθ／ρWgy₁(14)

式中，ψ_i：为土壤水的基质势；γ_t：水的表面张力；ρ_W水的密度；θ：接触角；g：重力加速度。

最终根据所取得的ψ_i～

即可得出某质地的水分特征曲线。

上述模型最关键的问题之一是确定(10)式中的a。在Arya和Paris(1981)的研究中，a值的确定是通过实测与计算土壤含水量，利用最小二乘法拟合得出的，这就给此模型的应用带来一定的困难。

那么不同质地土壤的a值到底反映了什么呢?有没有什么物理的含义?能否通过简单的办法求得a值呢?Tyler和Wheatcraft的研究工作解决了上述问题，并在机理上解决了从土壤机械组成分析的数据求出土壤水分特征曲线的分形数学模型。原理如下：

设土壤由大小不同的球形颗粒组成，那么孔隙通道就呈分形结构。设

为毛细管的真实长度，据(7)式得：

=F(2R₁)^1－D_p(15)

式中用2R₁替换了ε，D_p为孔隙通道的分形维数。

根据(6)式F为一常数，如取测量的长度为2R₁，即为直线长度

，在这种情形下，N_i=1，则：

　　　　　　F=hD_p　　　　(16)

合并(15)、(16)式得：=hD_p(2R₁)^1－n_p(17)

由(3)、(4)式可得：

　　　　　　hi=2R₁N₁　　　　(18)

把(18)式代入(17)式得：

　　　　　　道=2R₁ND_p　　　　(19)

那么，分形孔隙通道的体积为：

　　　　　　(20)

有效孔隙的半径为：

　　　　　　(21)

比较(10)式与(21)式，即可得出：a即为土壤孔隙通道的分形维数。从而说明了a的物理意义。根据分形几何学原理，设它分形维数为D，它的拓朴维数为D_T，则下式成立：

　　　　　　D_i=D－D_T＞0　　　　(22)

式中D_i为分形增量(fractal increment)。

利用(22)式可从原始分形过程来计算低于拓朴维数物体的分形维。如知道一个分形表面的D为2．5，那么D_i=2．5－2=0．5，如此就可计算出从分形表面所得到的一条剖面线的D=D₁+D_T=1+0．5=1．5。

如果把土壤中的孔隙视为穿过三维土体的一维通道。那么据(22)式即可求得(21)式中的D过程如下：

据(8)式，求得土壤颗粒分布的分形维数D，由于大小颗粒组成的土壤基质为一三维体。据(22)式：

　　　　　　D_i=D－3　　　　　　　　　(23)

再据(22)式，土壤孔隙通道的维数D_p为：

　　　　　　D_p=1+D_i=D－2　　　　(24)

到此，只要有土壤机械组成分析与容重的数据，据(8)、(24)、(21)、(11)、(14)式，即可求出此土壤的水分特征曲线。

3．分形理论在土壤结构研究中的应用。Bartoli等已报导了分形理论在土壤结构中研究成果。结果都表明，用分形维数D可定量地描述土块或土壤团粒(团聚体)的结构。

仿照(6)式，如：

　　　　　　m(R)∝R^D_m　　　　(25)

　　　　　　p(R)∝R^D_p　　　　(26)

　　　　　　s(R)∝R^D_s　　　　(27)

成立，则表明研究物体具有质量、孔隙度、表面积的分形结构。

(25)～(27)式中，R为研究物体的连长或半径，m、p、s分别为质量、孔隙度与表面积，D_m、D_p、D_s分别为质量、孔隙度与表面积的分形维数。

Bartoli等(1991)采用图象分析的方法，在10^－9至10^－1m尺度范围内，对自然土壤的切片进行分析，求出了粉砂质土壤的质量与孔隙度的分形维数D_m、D_p，利用水银孔隙度仪与分形立方块产生模型确定出了＜2mm风干样品的表面分形维数D_s。结果表明：土壤中不存在孔隙度的分形结构，但质量与表面积的分形结构是存在的，且在一定范围内，D_m与D_s成正比，与平均孔隙度成反比，与水稳性大团粒的含量成正比。

Young和Grwqford利用(25)式的原理，对田间原土样直接测量R与质量m(干重)，得出在不同耕作情形下有D_m值为2．75～2．39。

研究表明，土壤团聚体分形维数D受能量输入、作物耕作历史强烈影响，并应用分形理论建立了一不随标度而变的破裂模型来研究团聚体的稳定性。

4．分形理论在土壤溶质运移研究中的应用。从以上论述可知，土壤作为一个多孔的介质，是一种具有较典型分形特征的材料。如它的颗粒分布、孔隙通道形状、土壤团聚体、土壤颗粒的表面积、土壤孔隙的体积等都具有分形几何特征。这就导致了一个新研究领域，即如何把分形理论应用于多孔介质流体运动中去，解决其中困扰着人们的一些基础性理论与应用的问题。

现研究的主要热点集中在利用分形理论如何确定饱和导水率K、水动力弥散系数D。其中对水动力弥散系数D研究，水文地质工作者已做了一定的工作，报导了多孔介质水动力弥散度效应的分形特征。一般研究表明：野外测得的弥散度要比室内大，且野外弥散试验规模越大，弥散度也越大，即水动力弥散具有尺度效应。由于宏观弥散与微观弥散的机制是相同的，即多孔介质的非均匀性而造成流速不均匀为产生水动力弥散的主要因素，故弥散度反映了多孔介质骨架结构的特征长度。根据已有的文献报导，不同基准尺度下模拟所求出的弥散度见表2。

表2 溶质运移数值模拟所求出的弥散度

注：A一区域模型；C－剖面模型；O－维模型。

通过表2，可求出如下关系的直线：

(28)式表明，数值模拟中，弥散度a_L的尺度效应的分维是0．500。

用此种方法求出的尺度效应的分维，对研究多孔介质中水动力弥散具有重要意义。尺度效应分维作为一种定量指标，描述弥散度随尺度增加而增大的规律，为地下水污染的模拟、土壤中溶质运移的模拟提供了新的概念与方便的参数估计方法。

近几年来，Maloy等报导了分形理论在多孔介质中多相流中的应用，也值得土壤科学工作者重视。

5．区域土壤属性的分形特征。早在1981年P．A．Burrough根据Weiesstrass-Mandelbrot分形函数(WBF)、时间序列分析的方法、空间变异的研究方法，计算并报导了景观与其它环境数据的分形维数。其中土壤属性及相关因子的分形维数见表3。

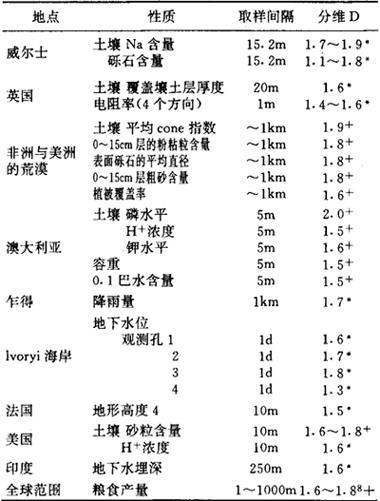
表3 区域土壤属性及相关因子的分形维数

*据半方差图计算，+据块方差计算。

从表3可以看出，在一定时空范围内，土壤属性具有分形特征，不同土壤属性具有不同的分形特征，并且研究尺度不同，同一土壤属性也表现出不同的分形特征。一般来讲具有分形特征的系统的时空动态上与混沌行为密切相联。这就进一步表明了区域土壤属性在时空系统中存在关十分复杂的行为。通过区域上有限点的数据重构区域土壤属性的分布图或者做到对某一土壤属性的较长期的预测是一项艰巨的研究工作。把分形理论以及混沌理论引入到对区域土壤时空性质的研究当中，可能有利于一些基础性理论问题的阐明。

6．分形理论在与土壤科学相关领域中的应用。分形概念最早是由Mandelbrot在探讨地学领域中的问题时提出的，如今已在地学研究领域中广泛应用。我国已于1992年5月召开了第1届全国分形理论与地质科学学术讨论会。其中利用分形理论的方法可以模拟地质体表面(地形起伏等)、各种地貌景观。土壤科学工作者在研究区域土壤的分布、利用及其规划、水土流失模型的建立等方面可借鉴此种研究方法与内容。

分形维数D也已在地理信息系统和遥感、制图学等方面开始应用，越来越受到关注。在景观生态方面，分形维数D可以对区域不同土地类型或景观类型分布的几何特征进行描述，对城市、乡村、海岸线区域所做的比较研究表明，TM影响上不同土地类型在不同波段具有不同水平的分形维数D，城乡区域D值最高，紧接着是海岸线和乡村区，O'Neill(1988)对美国东部景观格局指标的研究也表明，海岸带与森林景观多呈复杂的几何形状，D值高，而农业景观呈简单的几何形状，D值低。一般情形下，景观类型形状的D值为1．24～1．45。另外，作为一种指标，分形维数D可对区域某一变量动态分布预报模型的运行结果进行检验。

分形理论在土壤科学中应用展望从以上综述可知，仅仅几年时间，分形理论的应用几乎涉及到土壤科学的各个方面，表现出了诱人的应用前景。根据分形理论研究的对象结合现阶段土壤科学研究的特点，预计在近几年内，以下几个方面将是分形理论应用的活跃领域。

1．土壤结构的形成和破坏过程的模拟。虽然应用分形理论方法对土壤结构进行定量化描述还有许多工作要做，但是，人们更关心的是土壤结构动态演化过程，所以，如何把分形理论中的凝聚模型(如DLA)、破裂模型应用到土壤结构研究中，对土壤结构的动态演化过程进行模拟将是一个主要的研究方向。

2．土壤表面积的分形特性与土壤肥力的关系。众多实验已表明，土壤表面积具有分形几何的特征。这就要求人们改变传统的认为单位质量的土壤(干重)其表面积是一定值的观念。相应的对诸如不同分形特性的土壤，其中发生的吸附、交换、化学反应、生物过程等是否有规律可循?不同表面积分形特性的土壤其肥力特征如何?等问题尚需作进一步研究。

3．土壤水分运动参数、溶质运移参数的确定。应用分形理论，已建立了初步确定土壤水分特征曲线的模型，但还需不断完善。重点将放在：根据土壤为一具有分形特征多孔介质的特点，从理论和方法上来探讨如何确定其中水分的溶质的运移参数(K、D)以及它们空间变化特征。

4．土壤的分形特征与植物根系的生长发育。从形态上来看，作物的根系具有典型的分形特征。但有关根的分形特征与土壤的分形特征之间的关系，至今未邮研究报导。这方面研究对阐明SPAC系统中某些过程，根系对水分、养分的吸收有着十分重要的意义。

5．土壤属性时空变化规律的研究。仅仅确定出土壤属性时空变化的分形维数是不够的，还需从下面两个方面进行深入研究。(1)分形理论方法与空间变异性研究方法相结合．研究点到面的扩展、区域插值、区域土壤属性制图的定量化方法。(2)分形理论、混沌理论、时间序列分析等方法相结合，建立区域土壤属性在时间上变化的预报模型。

6．土壤属性的遥感解译。分形理论方法已用于图像的识别、存贮处理诸方面。应用分形理论方法可望解决遥感影像自动识别分类中对纹理的识别与定量化，结合区域土壤属性的空间分形特征，预计将会使区域土壤属性的遥感解译精度大为提高。

7．新的分形理论方法的引入。分形理论是一门发展中的学科，许多概念还在不断发展与深化之中。近几年来，多标度分形理论、分形动力学等各分支发展很快，土壤科学工作者应密切关注这些新动向，及时把它们引入到自己的研究工作之中；同时．争取在应用分形理论研究土壤科学过程中，对分形理论的发展作出贡献。

【参考文献】：

1 Mandelbrot B B．The Fractal Geometry of Nature，Freeman，San Francisco，1982

2 Tyler S W，Wheatcraft S W．Soil Sci．Soc．Am．J．，1989，63：789～996

3 Bartoli F，Philippy R，Doririsse M，et al．J．Soil Science，1991，42：167～185

4 Perfect E，Kay B D．Soil Sci．Soc．Am．J．，1991，55：1552～1558

5 Young l M，Crawford J W．J．Soil Scicece，1991，42：187～192

6 Turcotte D L．J．Geophys．Res．，1986，91：1921～1926

7 Mlaoy K J，Feder J，Jossang T．Phy．Rev．Lett．1985，55：2688～2691

8 Burrough P A．Nature，1981，294：240～2545

9 O'Neill R V，Krummel J R，Gardner R H，et al．Landscape Ecle．，1988，1：153～162

10 李国敏．多孔介质水动力弥散尺度效应的分形特征，第1届全国分形理论与地质科学学术讨论会交流论文，1992

(中国农业大学农业资源环境学院李保国教授撰)

随便看

科学参考收录了7804条科技类词条，基本涵盖了常见科技类参考文献及英语词汇的翻译，是科学学习和研究的有利工具。