【分维图形】
拼译：fractal
通称分形，是美国数学家曼德布劳特(B．B．Mandelbrot)根据拉丁文“Fractus”拼造的新词。1975年，曼德布劳特著文对分形的背景作全面论述，后于1982年出版的《自然界的分形几何学》被公认为是关于分形的基础性的著作。由此，曼德布劳特获1985年Barnad奖章。
分形的研究涉及许多领域。自然界的大量现象与分形有关，如海岸线、河流网络、肺膜、湍流、星团等，甚至某些社会经济现象的内在机制也与分形结构有密切的联系。就工程图学领域而言，针对不规则的几何体进行绘图，无论再生已存在的还是创造一类不存在的直观环境，分形几何都是一个有力的工具。分形的研究始于19世纪末。康托(G．Cantor)给出一类点集：将闭区间〔0，1〕3等分，去掉中间的开区间；再将余下的两段区间各自3等分并去掉各自的中间更小的开区间；继而对余下的4段更小的区间施行同样的操作，以此无限继续下去，基极限情形得到的点集，便是后来称为的康托三分集。它是分形的重要典型。德国科赫(von Koch)1904年给出雪花曲线，意大利皮亚诺(G．Peano)1890年给出一类充满平面正方形的曲线，波兰谢尔宾斯基(W．Sierpinski)给出具有无穷多开洞的“垫片”与“海绵”等，都是分形的古典例子，数学上著名的处处连续但处处不可微函数的维尔斯特拉斯(Weierstrass)反例以及物理学中的布朗(Brown)运动轨迹，也是分形研究关注的内容。迄今，分形的基本理论尚不完善。分形这个概念迄今尚无最后的科学定义。在曼德布劳特最初的论述中，定义分形为豪斯道夫(Hausdoff)维数大于拓扑维数的集合。按这个定义，某些应该作为分形来研究的对象，如著名的皮亚诺(Peano)“充满空间”的曲线等，被排除在外。因而他后来又修改了分形的定义，强调分形的某种自相似结构的特征。目前，按英国法克内尔(K．J．Falconer)的说法，一般认为具有下面典型性质的集合F为分形：(1)F具有任意小比例之下的精细结构。(2)F的不规则程度，无论表现在整体还是局部，都不能用传统的几何语言描述。(3)F通常有自相似结构(几何自相似性或统计意义下的近似自相似性)。(4)F可以被定义新的维数，这个维数往往大于其拓扑维数。(5)F可由迭代过程产生。近代非线性科学，特别是动力系统的研究更加深了对分形的认识，通过对复动力系统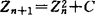
的性态研究，导致曼德布劳特集合与尤里亚(Julia)集合的发现，从计算机绘制的图形中就可观察到复杂精细的自相似结构。佩特根和黎赫特(H．－O．Peitgen，P．H．Richter)在计算机上对复动力系统给出184幅完美的分维图形，这项工作引起重视。分形紧密地与混沌(Chaos)现象联系在一起，其中富有启发性影响的是费根堡(M．Feigenbaum)对连续单峰映射的数值实验，当Xn+1=λXn(1－Xn)的参数λ增长时，序列｛Xn｝出现倍周期分岔(Bifurcation)，继而导致混沌，而在混沌发生的地带，仍出现复杂的有序对构，并从λ增长的速率发现δ=4．669201660910…这一常数(费根堡常数)。用计算机绘制分形，是20世纪80年代开始蓬勃发展的新课题，分形可以描述复杂非规则客体，因此在自然景物模拟、环境仿真、医学、生物、材料等科学领域成为有效的工具。一般来说，分形的生成要使用分辩率较高的快速计算机工作站(Computer workstation)，算法上往往是以递归方式通过迭代过程实现，其中迭代函数系统和L－系统是目前流行的两类基本算法，IFS的基本思想是通过一族压缩映射定义唯一非空的不变集，如此的不变集通常都是分形，从这种方法中，又发展了一系列压缩映射族中的映射随机选取的技巧。IFS的思想虽然早就存在，但首先系统地用于分形绘制的研究是由胡钦森(J．E．Hutchinson，1981)给出，曼德布劳特(1982)、狄克英(F．M．Dekking)、巴恩斯利与戴姆柯(M．F．Barnsley，S．G．Demko，1985)等人成功地绘制了山脉、树木等美丽的仿真图形，甚至通过少量的信息绘出完整的人像。L－系统基本概念由美国林丹梅耶(A．Lindenmayer，1925～1989)提出，后经数学家和计算机科学家发展成一套形式语言系统。L－系统的核心是边改写与节点改写规则，利用字符串表达一个初始图形，并对字符串每个字符赋予特定的含义，然后递归地对某些字符施行给定的嵌入替换，逐次得到更长的字符串，这一系列的字符串便是图形在不同尺度上精细结构的编码。L－系统首先在植物生长模拟中取得成功的应用，事实上，它对平面及空间的复杂结构的绘制(如电子线路，物质结构)提供了可行方案，IFS与L－系统在图形与图象中数据压缩方面的意义是不容低估的。分形被用于自然景物仿真及动力系统的过程模拟，往往通过计算机屏幕上逐次开“窗口”放大，动态地演示精细结构，这便是在电影及电视动画中的应用。20世纪70年代以来，计算机动画在欧美及日本发展迅速，每年一度的欧洲图形学专业学术会议及美国SIGGRAPH会议集中反映这方面的成就，其中大量的作品出自分形绘制手段。(北方工业大学齐东旭教授撰)