【BCH－代数】
拼译：BCH-algebra
是由胡庆平于1981年引入、并由日本井关清志定名的一类抽象代数。经过胡庆平和一批同行10多年不懈的努力，迄今已建立了BCH－代数理论的框架，确立了一批专题，明确了一些主要方向，得到了一些结果，使之成为较活跃、正在迅速发展的现代代数的一个分支。
1966年，日本的依美和井关清志引入BCK－代数。如果＜X；*，0＞是一个(2，0)型代数，且满足下列公理：对于任意的x，y，z∈X， k－1．((x*y)*(x*z))*(z*y)=0， k－2．(x*(x*y))*y=0， k－3．x*x=0， k－4．0*x=0， k－5．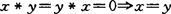
，则称＜X；*，0＞为一个BCK－代数。1966年井关清志引入了BCI－代数，即(2，0)型代数＜X；*，0＞，满足下列公理：对于任意的x，y，z∈X，成立
I－1=K－1， I－2=K－2， I－3=K－3， I－4=K－5， I－5．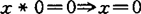
．1980年胡庆平和井关清志合作研究结合BCI－代数，即具有性质(Ass．)(x*y)*z=x*(y*z)
的BCI－代数＜X；*，0＞，其中x，y，z是X中任意3个元素。结合性是1966年引入BCI－代数以来发现的关于BCI－代数的第1个固有性质。在研究结合BCI－代数的同时，胡庆平得到了BCI－代数的下列特征：设＜X；*，0＞是一个(2，0)型代数。则＜X；*，0＞是一个BCI－代数的充要条件是它满足I－1，I－3，I－4和下列条件：
(p－1) (x*y)*z=(x*z)*y，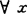
，y，z∈X
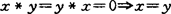， H－3．(x*y)*z=(x*z)*y，其中非空集合X称为BCH－代数＜X；*，0＞的基础集合。自1981年以来，胡庆平和一批同行对BCH－代数作了很多研究。在井关清志的大力支持下，关于BCH－代数较早的论文发表在日本；以后国内的一些杂志陆续发表了一批关于BCH－代数的论文；而胡庆平将BCH－代数理论的基本框架写成专章发表，这是在专著中第1次出现对BCH－代数的介绍。美国的Math．Reviews及德国的Zentbl．Math．均对作者引入的BCH－代数作了介绍，使国内外一些数学工作者对BCH－代数产生兴趣，并进行学习和研究。
10多年来对BCH－代数的研究表明，这是十分必要的。首先，BCH－代数是一种独立的公理代数体系。1987年胡庆平和杨永保证明了BCH－代数的3条公理H－1，H－2和H－3互不蕴涵，因而BCH－代数公理系统是独立的。其次，BCH－代数类是比BCI－代数类较大的一个代数类。易知成立下列包含式：BCK－代数类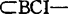
代数类
代数类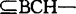。前一真包含式是井关清志在1980年给出的。而1983年胡庆平和李新给出了第1个真BCH－代数的例子，从而BCH－代数类真包含BCI代数类。第三，存在无限多个真BCH－代数，而且一切真BCH－代数已构成一个真类。第四，产生了一批新问题，如胡庆平在1983年就提出了关于BCH－代数的一系列值得研究的问题：BCH－代数类和范畴BCH的研究、BCH－代数性质的研究、BCI－化和BCK－化的研究、理想和自然的二元关系≤的研究及某些BCH－代数类的研究等。第五，已经有了初步的应用，如胡庆平已将BCH－代数用于泛代数的研究。随着BCH－代数理论的不断丰富和研究的不断深入，逐步出现了一批研究BCH－代数的专题。从目前来看，研究BCH代数的主要专题有以下8个：(1)对于关系≤的研究。实际上，＜X；*，0，≤是一个关系系统，其中
，因而有一系列需研究的问题，例如BCI－代数的自然半序的结构，BCH代数的关系≤，及由BCH－代数导出的一类关系系统等。(2)新代数的生成的研究。如子代数、积代数、并代数等，而合理的商代数问题更是研究的一个热点。(3)某些BCH－代数类的研究。本质上是同构分类问题的需要，是一个很重要的问题。(4)扩张问题研究。主要有：把井关清志的BCK－代数的“一点扩张”(为BCI－代数)推广为“一点直接扩张”(为真BCH－代数)；真BCI－代数的一点扩张(为真BCH－代数)；真BCH－代数本身的一点扩张；以及进一步的问题，如多点扩张、并集扩张及限制或“减点”问题等。(5)基数函数和序数函数研究。本质是用数量的方法研究BCH－代数。(6)簇和亚簇。主要考察BCH－代数类及其各主要子类哪些是簇或亚簇，及作为簇或亚簇具有什么性质或相互关系。(7)结构问题。从目前来看需要解决的问题很多，如BCH－代数的代数结构、具有自然半序≤的BCH－代数的序结构、不具有自然半序的关系≤的结构、各类代数本身结构的特点等。(8)同态和同构问题研究。如不变性问题、与生成子代数的关系、与各代数类的关系、同态和同构定理研究，尤其是同构分类问题的研究等。研究BCH－代数的方法主要有5类：(1)集合论方法，主要有数量方法(如基数和序数的使用)，论证方法(如使用各种归纳法)、公理方法(如利用选择公理，或连续统假设)、子集方法(如包、核、闭包系统)等。(2)范畴论方法。主要使用范畴、函子、自然变换、伴随、万有性质、交换图等；(3)泛代数方法。如一般到具体的方法，以格、多项式、闭包系统为工具研究代数结构的方法，以合同关系建立商代数的方法，泛代数的某些专题(如簇论、扩张理论等)引伸到BCH－代数的方法等。(4)经典代数的方法，在半群、群、环、域、格、模等代数系统研究中采用的方法也可应用于BCH－代数的研究，如在BCH－代数中研究理想、根、根性、素性、分解等。(5)其它方法。如拓扑学中的方法(一点扩张、一点完备化)、拓扑群的方法(拓扑代数)、同调的方法(同调BCH－代数)、线性代数的方法(环式BCH－代数)等。BCH－代数还有丰富的外延理论。BCH－代数范畴BCH，这是BCH－代数和范畴论结合的产物，主要研究BCH的性质、有关BCH的一些问题和BCH的子范畴等。同调BCH－代数，这是同调代数与BCH－代数结合的产物。环式BCH－代数，这是BCH－代数与环论、线性代数结合的产物，主要研究性质、矩阵及其它有关问题。BCH－拓扑代数，这是BCH－代数和拓扑学结合的产物，主要研究几个有关的代数问题、有关的拓扑问题及其它进一步的问题。预计，BCH－代数理论研究今后10年中的主要热点应是：BCH－代数的结构、主要的专题和主要的外延方向，估计基础理论研究仍将围绕着结构、分类、基数、四基(点、子集、子类、簇)等展开，并将进一步着手应用问题的研究。【参考文献】：1 Imai Y，et al．Proc．Japan Acad，1966，42∶19～222 Iseki K．Proc．Japan Acad．，1966，42∶26～293 Hu Qingping，et al．Math，Sem Notes，1980，8∶553～5554 胡庆平，等．科学通报，1982，12∶714～7165 Hu Qingping，et al．Math，Sem Notes，1983，11∶313～320。6 Hu Qingping，et al．Math，Japonica，1985，4∶659～6617 胡庆平．BCI－代数．西安：陕西科技出版社，19878 胡庆平，等．西北大学学报，1987，2∶58～629 胡庆平．数学季刊，1989，3∶104～10610 胡庆平等．西北大学学报，1990，1∶18～30(西北大学胡庆平教授撰)