【板形理论的研究】
板形控制技术的发展，促使人们对板形控制的理论基础——板形理论进行系统深入地研究。其目的是建立各种影响因素与板形之关系的数学模型，以便准确地预测、设定和控制板形。因轧后的板形取决于轧件在辊缝中的三维变形，而其变形又与轧辊的变形有密切关系，控制板形前需对轧后板形预先做判别，即需研究板形的判别模型，故完整的板形理论研究内容应包括：(1)轧件三维塑性变形的计算模型——金属模型；(2)辊系弹性变形的计算模型——辊系模型；(3)轧后带材失稳屈曲变形的计算模型——判别模型。这3个模型相互联系，不可分割。
对板形控制来说，研究金属三维变形最重要的目的是确定轧制压力和前、后张力等横向分布的数学模型。因为轧制压力的横向分布直接影响辊缝形，前张力的横向分布直接反映轧后板形状，前、后张力的横向分布通过影响轧制压力而影响辊缝形状。1．三维解析法。户泽等提出的三维解析法的基本思想，是把纵向(轧向)和横向平衡微分方程都取差分形式，再与塑性条件、塑性流动方程、体积不变条件和边界条件联立，用数值法和迭代法求出三向应力在变形区的分布和板边形状曲线。对宽板的计算，宽展的误差很大，约是实验值的2倍；前张力横向分布误差也大。户泽等关于宽板的理论模型存在两个问题：(1)将横向平衡微分方程用积分方程代替；(2)将板边力边界条件横向正应力σy=0改为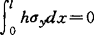
且不考虑剪应力τxy=0的条件，式中h、l分别为变形区轧件厚度、长度。连家创等(1984)对户泽模型做了改进，在粘着区用预位移原理计算摩擦力，使横向平衡微分方程更精确；并在板边用精确的力边界条件(σy=0，τxy=0)，完成了宽板的计算，但需由经验确定剪应变修正系数。2．有限元法和边界元法。刘才(1986)和杜凤山(1990)等用三维弹塑性有限元法研究了厚板(H=25．4mm，宽厚比3)和薄板(B=50～30mm，H=2～0．4mm)的轧制过程，给出了变形区三向应变和单位轧制压力、两向单位摩擦力的分布。但除轧制压力外，计算未与实验结果定量对比。肖宏(1991)用三维弹塑性边界元法研究了带张力冷轧(B=240，200mm，H=2，0．7mm)问题，前、后张力横向分布计算与实验结果基本吻合，其余未做对比。3．条元法。刘宏民(1988)用条元法，据能量原理优化求解横向位移函数的数值解，进而确定变形区内的流动速度场、应变速度场和应力场等。冷轧带材(B=250mm，H=0．4mm)轧制压力、两向摩擦力和前、后张力等横向分布计算与实验结果吻合较好，在板带材轧制理论方面取得了重要进展。三维解析法及有限元法和边界元法虽从理论上可对金属的三维应力与变形做较详尽的描述，但计算量大，仅适于研究宽厚比较小的厚板或板坯轧制问题；而对宽厚比很大的薄板带的研究，不但单元数目和计算量大增，且很难得到正确可靠的结果。而条元法据带材轧制的特点，引入一定的合理假设，将研究的问题降维而大量减少计算量。在大宽厚比的条件下，各力参数横向分布计算与实验结果吻合较好，适用于对板形问题的分析。今后应在更广泛的轧制条件下研究、检验该法的适用性，使其不断发展和完善。辊系的弹性变形沿轧件宽度是不均匀的，这是决定板形的重要因素之一。随液压弯辊、轧辊轴向移动技术的应用，辊系变形的理论计算空前活跃。(1)整体模型法。一种是由M．D．Stone(1965)提出、后经别人改进的弹性基础梁法，其出发点是将支承辊视为弹性基础，工作辊视为支承在弹性基础上的梁，通过求解四阶常微分方程确定工作辊的挠度。该法考虑了辊间的压扁不均，但视支承辊为弹性半空间并用文克尔假设，不符合实际。另一种是双层梁法，其特点是分别计算工作辊和支承辊的挠度，据变形协调方程、力平衡方程确定辊间压力和压扁量的轴向分布。力学模型比较接近实际，但需对辊间压力的轴向总体分布规律做假设，故计算精度不高，适用性不强；而且，未解决好辊间压扁变形的计算问题。(2)分割模型法。K．N．Shohet于1968年提出的分割模型法，是将连续分布的力与变形离散化，以力为未知量，根据变形协调方程和力平衡方程解出轧制压力、辊间压力和变形量的分布。因该法对力的轴向总体分布不做任何假设，故适于载荷任意分布的计算。但该法也未解决好辊间压扁变形的计算。(3)有限元法和边界元法。因这两种方法可详尽地描述整个辊系的应力和变形，故对板形分析和轧辊强度分析都有意义。但因其计算量过大，且因辊间接触宽度极小而使其压力和压扁计算困难。在辊系弹性变形的计算中，辊间弹性压扁的计算是个难点，也是长期未解决好的问题。主要有半平面和半无限体两种计算模型。前者忽略了相邻区域压力和轴向应力的影响，后者扩大了辊身端部以外部分对压扁变形的限制作用。以轧辊受轴向均布载荷为例，两种模型的计算结果与实际压扁变形分布均有较大差别。于秋林等(1986)用有限梁迭合法较好地解决了支承辊弹性压扁的轴向分布；但却未解决工作辊的压扁问题。轧辊热变形理论是辊系弹性变形理论的重要分支。有关辊系热变形的计算主要有解析法、差分法和有限元法。从深度和广度看，此项研究相对落后，其难点是不能准确地给定边界条件。故精确地确定边界条件是今后研究的重点。成卷带张力板带轧制生产中，前张力的横向分布是不均的，消除张力后将转化为残余应力，该值超过极限将使带材产生失稳，若失稳则屈曲变形。板形判别模型的任务是据残余应力的分布判别带材是否失稳，若失稳，计算出失稳后的波浪度，再据波浪度是否超限而决定是否需调节板形。薄板带材的失稳，属大挠度屈曲变形问题。因此时板带材的挠度常大于其厚度。连家创等(1987)用大挠度屈曲变形理论，根据能量原理研究了冷轧带材单边浪、中间浪、双边浪等问题。按该文的方法对不同的浪形需设定不同的挠度函数，因而其计算方法不具有一般性和通用性，给实际应用造成困难。I．Takashi等(1987)用有限元法研究了中间浪和双边浪的情况。目前尚未见到复合浪的研究成果。板形理论是内容广泛、难度较大的研究领域。尽管某些研究成果已用于实际，但从整体看，仍处于研究阶段。目前辊系模型的计算精度已基本达到可实用的程度，今后需进一步研究辊间压扁变形的计算精度和轧辊的热变形。金属模型是板形理论中的一个难点。塑性变形问题的复杂性，决定金属变形的分析要比辊系变形的分析困难得多。为使辊系变形的研究成果更好地用于板形控制，在研究金属三维变形的基础上，尽快建立轧制压力和前、后张力等横向分布的数学模型，已成为技术发展的迫切要求，应成为今后的重点攻关内容。有关板形理论分支模型的研究很多，整体模型的研究极少。I．Takashi等(1987)将金属模型、辊系模型与判别模型联立起来，完成了整体模型的计算，开创了一个先例。分支模型的研究已有大量成果，开展板形理论的综合研究，建立整体模型的条件已基本具备。大力开展整体模型的研究，开发出有实用意义的软件，进而获得便于应用的简化模型，应成为板形理论研究的大方向。(燕山大学刘宏民撰)