【大系统理论】
拼译:large scale systems theory
自20世纪70年代开始,大系统理论逐渐形成了一个专门领域。它综合了近代控制理论、控制论、图论、运筹学和决策论等方面的成果,是系统工程的理论基础之一。
大系统一般是指规模庞大(模型的维数很高)、结构复杂(多层次,互关联)、目标众多(目标间有冲突)、时标各异(同一系统内有多个时标)、地理位置分散、并常常具有随机性和不确定性的复杂系统。它不仅把复杂的工业系统作为研究对象,而且已扩展到社会、政治经济和生态环境等系统中。大系统理论涉及大系统模型简化、大系统结构、大系统稳定性以及大系统的递阶和分散控制等理论。国内外已把大系统理论成功地应用于电力系统、城市交通网、数字通信网络、计算机集成制造系统(CIMS)、生态系统、水资源系统和社会经济系统等各方面。1.大系统模型简化。由于大系统包含的元件多,元件之间关联复杂,输入和输出的数目也很多,建立大系统精确数学模型不仅困难,而且计算很复杂,因此需要对大系统的数学模型进行简化。通常采用的方法有集结法和奇异摄动法。所谓集结,就是把原系统中众多的状态变量按线性组合,合并成数量较少的新状态变量。集结后的简化模型保持了原模型中主导特征值,使简化后模型的动态特性与原模型的动态特性无很大的差异。如原模型的阶次为n,集结后简化模型的阶次为m(n>m),m的选择是集结法简化模型的关键,实质上也是一个系统阶次的辨识问题。1968年青木(M.Aoki)首先用集结法简化大规模动态系统。用奇异摄动法简化大系统模型是科科托维奇(P.V.Kokotovic,)在1972年提出的。所谓摄动是指系统数学模型中某些数量级较低的小参数的变动。当小参数摄动不致严重地改变系统动态特性时,称为正则摄动,它可以用来简化“弱耦合”的大系统。用小参数摄动研究系统某些特殊情况下的特征,称为奇异摄动。用奇异摄动法来简化“紧耦合”大系统,把大系统动态过程中快变模和慢变模分开,先略去快变模,使系统简化,然后用“伸长的时标”计算边界层校正,加入快变模的效应,以改进逼近度。2.大系统结构。大系统结构取决于组成大系统的子系统集合和各子系统之间的关联。大系统的结构决定了大系统的功能,不同的结构就产生不同的总体功能。由于大系统的受控对象分散,变量数目多,关联复杂,不宜采用集中式结构。在各种工程和非工程的大系统中,存在着2种基本结构:即递阶结构(层次结构)和分散结构。在递阶结构中,整个大系统分成独立平行处理的许多子系统,而且用一个协调器来协调各子系统之间关联。通过上级(协调器)和下级间重复的信息交换实现协调过程。原则上协调器可以拥有局部控制器所有的全部信息。所以递阶结构具有“经典信息模式”。在分散结构中,各子系统独立工作,整个系统不存在协调器。各子系统只拥有局部信息,它只能通过各子系统之间的信息交换来调整总体目标,故分散结构具有“非经典信息模式”。按研究问题的目的,子系统的分解和分级有不同的方式。从控制的角度出发,递阶结构又可分为多重递阶结构、多层递阶结构和多级递阶结构。多重递阶结构是按大系统模型的不同抽象程度来划分的,其结构如图1所示。多层递阶结构是按大系统控制和决策的性质的复杂程度来划分的,其结构如图2所示。在多级递阶结构中,互相关联的许多子系统按一定的支配关系来排列。下级决策单元受上级决策单元的干预和影响。系统的目标可以是单一的,也可以是多个的。图3是一个多级多目标的递阶结构意图。3.大系统稳定性。判断、分析大系统能否正常稳定运行的理论和方法是大系统稳定性研究的主要内容。考虑大系统稳定性问题一般分为3个步骤:(1)把给定的大系统分解成若干小规模的子系统;(2)利用经典的稳定性理论和方法分析各子系统的稳定性;(3)把所得的结果合起来,并将各子系统之间的相互关联作为约束条件,推导整个系统稳定性的判据。根据稳定性定义的不同,分析大系统稳定性的方法主要有2种:(1)李雅普诺夫(ляпунoв)函数法。对各子系统假设一个李雅普诺夫函数,然后利用向量李雅普诺夫函数理论;或者把各子系统的李雅普诺夫函数加权求和,构造标量李雅普诺夫函数来检验整个系统的稳定性。(2)输入输出法。将各子系统在泛函空间上用一个数学表达式或算子来描述,然后用泛函分析方法来进行大系统稳定性分析。在互连的大系统稳定分析中,主要的研究问题是:互作用的幅度和强度究竟可以达到多大,才不影响整个系统的稳定性。4.大系统递阶控制。递阶控制的概念是在70年代由米沙罗维奇(M.K.Mesarovic,)等人提出来的。根据受控对象的性质,分成稳态大系统递阶控制和动态大系统递阶控制。前者适用于过程变化较慢的工业系统,它关心的是稳态工况的优劣,按给定的指标决定最优的稳态工作点;后者关心的是系统的动态品质,按给定的指标决定最优的状态轨迹。递阶控制的基本思想是将大系统分解成若干相对独立的子系统,并构成控制系统的下层,而用上层的协调器来处理各子系统之间的关联作用。不论是稳态还是动态大系统,协调所采用的方法主要有:(1)关联预测法。按此方法,协调器要预测各子系统的关联输入和输出变量。下层各决策单元按预测的关联值求解各自的决策问题,然后把达到的性能指标送给协调器,协调器再修正预测值直到总体目标达到最优为止。由于在协调过程中模型中引入了约束,这方法也称模型协调法。这个方法的中间结果是物理上可实现的,因此也叫可行分解法。(2)关联平衡法。这种方法在下层各决策单元求解自己优化问题时,不考虑关联约束,而协调器则要通过干预信息来修正各决策单元的优化目标,以保证最后关联约束得到满足。这时目标修正项的值也趋于零,达到原目标的最优值。此方法也称目标协调法。其中间结果不能施加于实际系统中,故也叫不可行分解法。5.大系统分散控制。分散控制的主要特点是将复杂的大系统按其分布划分成许多独立子系统,分别用独立的局部控制器来控制。每个控制器只观测系统的局部输出,且只控制系统的局部输入,共同完成大系统所要达到的目标。分散控制系统分为分散随机控制系统和分散确定性控制系统。由于分散控制系统具有非经典信息结构它使得分散控制系统最优决策复杂化,成为非线性。即使对于最简单的线性二次型高斯(LQG)问题,分离定理也不再成立,反馈律也是非线性的。只有在特定的信息结构下,例如一步时延共享信息结构或具有嵌套的信息结构,分离定理才成立,并存在唯一线性最优解。在分散确定性控制系统中,其研究的理论主要包括分散系统的状态估计、能控性、能观性、稳定性和分散控制系统的镇定和极点配置,分散最优控制等。70年代初,戴维逊(Davision)和王(Wang)提出了分散固定模的概念,为系统地分析和设计分散控制系统提供了重要依据。以此为依据以后发展了各种扰动和参数摄动的分散鲁棒控制和结构摄动的分散鲁棒控制的理论和方法。
图1多重递阶结构示意图
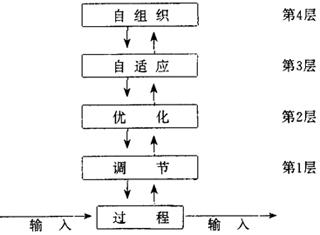
图2 多层递阶结构示意图
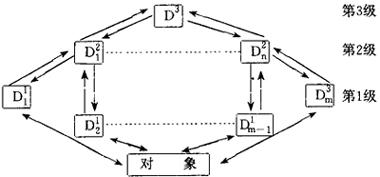
图3 多级多目递阶结构示意图
【参考文献】:1 李人厚,邵福庆.大系统地递阶与分散控制.西安交通大学出版社,1986.32 Mohammad Jamshidi modeling and controt,Elsevier Science Publishing Co.,19833 李人厚,胡保生译.分散控制,北京:国防工业出版社,19854 Siljak D D.Decentraliged Control of Complex Systems,London:Academic Press Limited,1991(西安交通大学李人厚教授撰)