【作物水分生产函数】
拼译：crop water production function Y
农业生产是一个十分复杂的大系统。由于在投入生产资源中存在着许多无法控制的或不能计量的变量，它们与作物产量的因果关系并不完全清楚，不可能构造出一个反映众多变量的完整的生产函数。所以，现有的农业生产函数多从实用目的出发，选择一个或少数几个投入因素作为自变量，其他因素维持常量，作物水分生函数即属于这种类型。
作物水分生产函数所反映的只是水与作物产量之间的技术、经济数量关系，即Y=f(W)。式中，W为水的投入量或能反映作物水分状况的某种物理量；Y为产量出量，即作物产量。作物水分生产函数可以定量地确定作物不同生长期对水分需求的反映，为制定灌溉水量最优分配决策提供必要依据。建立作物水分生产函数模型，首先要选定其因变量和自变量。因变量只有一个，即农作物产量。自变量可用能反映作物水分需求的物理量，如蒸发蒸腾量(简称腾发量)。在一定气候、土壤、作物条件下，腾发量大时光合作用强，产量就高。早在1958年，德威特(De Wit)就提出作物产量(Y)与蒸腾量(T)及水面蒸发量(E0)之比值有成正比便增长的线性关系，即Y=m(T／E0)，式中m为反映作物适宜水分和天气状态的综合系数。现有的作物水分产生函数模型多以腾发量或其相对值(实际腾发量与最大腾发量之比)作为自变量。许多学者，如弗林(Flinn，1970)、席勒和克拉克(Hiller and Clark，1971)、哈根和斯图尔特(Hagan and Stewart，1973)、道奈(Downey，1972)和雅隆(Yaron，1972)等都对腾发量ET与产量Y之间的关系进行过研究，指出当实际腾发量ETa等于最大(潜在)腾发量ETm时，即作物需水量得到完全满足时，只要其他环境条件无任何障碍，就能获得最高产量；而当ETa＜ETm时，由于土壤水分不足，作物出现水分胁迫(Stress)，产量将会降低。美国加里福尼亚大学(戴维斯)、亚立桑那大学(尤马)、科罗拉多州立大学(科林斯堡)和犹他州立大学(洛根)的联合试验(1971～1977)结果，也证明了这一关系的存在。在供水受限制的条件下，可以按作物全生长期内总供水量满足作物最大需水量(ETm)的程度及其对最终产量的影响，来确定作物水分生产函数。这种生产函数通常是以产量反映系数(Ky)来解释相对产量的下降数(1－Ya／Ym)与全生长期相对腾发量差额总量(1－ETa／ETm)之间的关系，可以写成(1－Ya／Ym=Ky(1－ETa／ETM)(斯图尔特，Stewart，1977)。大部分作物的相对产量(Ya／Ym)和相对腾发量(ETa／ETm)之间呈直线关系。事实上，作物各生长阶段对缺水的瓜是不相同的，甚至前一生长阶段的缺水还会给后一阶段作物的生长发育产生不利影响。因此，按全生长期总供水量所建立的作物水分生产函数，不能反映不同生长阶段及多次缺水对作物产量的影响。许多学者相继提出了以分阶段供水量为基础所建立的作物水分生产函数模型。这类模型的共同假定是；各阶段缺水均对作物生长发育不利，最终形成产量降低；全生长期由缺水造成的减产，是各个生长阶段缺水效应的综合结果。其代表性模型可归纳为3类：乘法模型 这种模型以乘法形式反映各阶段缺水效应之间的联系。第一阶段的缺水不仅影响本阶段，还对后续阶段产生影响。若其中一个阶段严重缺水，相对腾发量接近于零，则最后形成的产量亦接近于零。詹森(M．E．Jensen，1968)提出的公式为：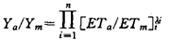
式中λi表示作物对i阶段缺水的敏感指标，该公式在世界各地得到广泛应用。约素(Hill Jonnso)和赖安(Ryan)(1979)考虑作物因倒伏或晚播种对产量的影响，将詹森公式修改为：
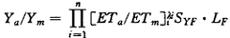
式中SYF为季节产量系数，用以反映晚播种对产量的影响，LF为倒伏系数，反映作物倒伏对产量的影响。在乘法模型的研究中，敏哈斯(Minhas，1974)等人做出了重要贡献，他们研究了由有效土壤含水量推算相对腾发量的方法，并将生产函数写成：
=a［1－(1－1－X1)2］b1［1－(1－X2)2］b2…［1－(1－Xn)2］
式中Ya为实际产量，X1为第i阶段的相对腾发量，a、bi为参数。这种生产函数具有两个重要性质：只要有一个阶段的相对腾发量为零，作物就绝产；相对腾发量由0向1递增时，边际产量(
)则由最大值向0递减。该生产函数曾利用印度新德里的小麦试验资料和美国俄亥俄州的苜蓿试验资料进行过验证，其计算值与实测值很接近，精度可达98．7%。
，式中βi为i阶段的敏感性参数。美国科罗拉多州科林斯堡等试验站的试验结果表明，斯图尔特的加法模型具有较高的精度。布朗克(H．Blank，1975)使用科罗拉多州立大学的试验资料验证了詹森的乘法模型，可用简单的加法模型表示为：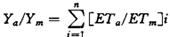
式中，Ai为第i阶段作物敏感性参数，用线性回归法求得，该法的计算结果与詹森的乘法模型十分接近。
积和综合模型 这是由加法与乘法两类模型综合而成的，也可看成是加法模型的新发展。《第12届国际灌排大会论文集》第1卷(1984)中，保加利亚学者提出用3项积和式建立产量增值与阶段供水的函数关系，即：
(武汉水利电力大学袁宏源教授撰；刘肇祎审)