【电磁场数值计算及应用】
拼译:nvmerical calculation in electromagnetic field and application
利用计算机,采用数值方法解电磁场问题,是自70年代发展起来的一门新学科,问题深入到工业生产的各个领域。 1856年麦克斯韦从数学的推演出发,以积分和微分的形式描述了电场和磁场之间的相互关系,得到了举世闻名的麦克斯韦方程组。百余年来,人们以此为出发点,从事着电磁场的理论分析与工程计算和设计。
可以归结为求解边值问题的泊松,拉普拉斯方程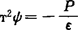 或T2ψ=0(偏微分方程)过去通常有两类方法:(1)严格解析法或称为解析法。经典方法有求解偏微分方程的分离变量法和求解积分方程的变换数学法——格林函数法。(2)近似解析法或称为近似法。在数理方法中,主要的有逐步逼近法、微扰法、变分法和迭代变分法。还有采用高频技术的几何光学法、物理光学法、几何绕射法(GTD)等以上解析法只能求解一些典型的问题。许多算法只适用于二维和稳态问题,不适用于不均匀和非线性问题,另外需花费一定的精力寻求特殊的算法和技巧。而实际电磁场的问题相当复杂。 或T2ψ=0(偏微分方程)过去通常有两类方法:(1)严格解析法或称为解析法。经典方法有求解偏微分方程的分离变量法和求解积分方程的变换数学法——格林函数法。(2)近似解析法或称为近似法。在数理方法中,主要的有逐步逼近法、微扰法、变分法和迭代变分法。还有采用高频技术的几何光学法、物理光学法、几何绕射法(GTD)等以上解析法只能求解一些典型的问题。许多算法只适用于二维和稳态问题,不适用于不均匀和非线性问题,另外需花费一定的精力寻求特殊的算法和技巧。而实际电磁场的问题相当复杂。 自从高速、大容量电子计算机引入电磁场领域之后,给电磁学开辟了新的前景-数值法。数值计算法的主要特征是将微分、积分方程中所作用的连续函数离散化,将微分方程化为差分方程,或将积分方程中的积分化为有限和,从而建立代数方程组,并利用松驰和迭代等技巧求解,原则上适用于任何复杂边界,精度高,缺点就是答案正确与否需要实验或其它可靠的结果来证明。短短的20年,数值法已深入到工业生产的各个领域,解决的面愈来愈广,分析的问题亦日趋复杂,已从线性场到时变场;从稳定场到瞬变场,从单一物理场发展到多种物理场的耦合场。此外,位函数和场强的计算精度也有了很大提高,其中尤以后者的进展更为工程界所关注。从20世纪40年代开始就有人试探用数值方法解决具有简单边界形状的场问题,此时有限差分法(FDM)已广为应用。虽然更早可以追溯到高斯时代,对于一维问题,早在1868年,莫尔(Mohr)在求梁的挠度时所用的图解弦线多边形法,就是完整的有限差分法。最早应用于二维问题,是1908年由龙格作出的。由有限差分法得到的大型代数方程的解法也同时得到了发展。这些发展源于高斯、雅可比(.Jacobi)(和赛得尔(Seiael)的基本贡献,以理查德(Richardson)和莱布曼(Liepmann)在迭代领域里的成果,高斯、杜里特(Doolittle)和乔英斯(cholεski)在直接法领域里的成就为基础。而真正使用差分法解决电磁场问题,是从1964年Winslow利用向量位,采用有限差分法离散,求解了二维非线性磁场问题开始。随后,Colonias和Dorst用该程序设计了同步加速器磁铁,并且把它发展成为TRIM软件包。此后采用有限差分法计算线性和非线性二维场的程序如雨后春笋般地在美国和西欧出现,如LINDA、MARE和NUTCRACKER等等。有限差分法简单、直观,无论是常微分方程还是偏微分方程,各种类型的二阶线性方程,以致高阶或非线性方程,均可利用它转化为代数方程组再求其数值解。其基本点是:基于差分原理,用离散点(节点)所组成的网格来代替连续区域,仅在每个离散点上算出未知量。例如用“差商”来近似代替导数和积分并作为各节点值的函数,把连续函数转化为离散方程。其最大缺点就是网格只能采用规则的形式:如矩形等,使得网格与边界和交界面形状不能拟合,不太适合于场的变化十分剧烈的问题,不适用于曲线边界和交界面。尽管有这些不足,但在1970年以前,实际上已占垄断地位,例如科罗拉多大学爱尔德莱小组以及弗里茨、缪勒和塞尔夫在交流发电机和直流电机上都采用它。目前各种数值计算方法应运而生,并相继应用到各类电磁场问题中。1.有限单元法(FEM)。也简称有限元法。以变分原理和剖分插值为基础的一种数值计算方法。能量泛函的欧拉方程就是与泊松方程吻合而转化为求泛函的极值解-变分问题。在FEM中,把整个场域剖分为许多单元,每个单元用合适的插值函数来表示一未知量,可生成一组代数方程组,然后再用直接法或迭代法即可求出各个节点的位值。早期广泛应用于拉普拉斯方程和泊松方程所描述的各类物理场。此后证明,应用加权余量法中的迦辽金法或最小二乘法等同样得到了有限元方程,因而可用于任何微分方程所描述的各类物理场,同样适用于时变场,非线性场以及分层介质中的电磁场求解。适用于具有复杂边界形状或边界条件、含有复杂媒质的定解问题。特别是近10年来,由于数值处理技术的提高,例如采用不完全Cholesky分解法或新的预处理共轭梯度法、采用自适应网格剖分、坐标变换和形状函数的应用、标号寻优、边界寻优等方法,使得有限元法在电磁场数值分析的领域中,越来越占有主导地位。当然也存在不少问题,得到代数方程组元数大,需借助大、中型计算机,特别对三维问题尤感不便。对无限区域中的求解问题不易处理。2.边界元素法(BEM)。为了克服有限元的缺点,人们寻求和发展了边界法。所谓边界元素就是把区域的边界分割成许多元素,在元素上所考虑的插值函数,可以有种种形式。“边界元素”这个词,首先在20世纪70年代由英国的Southamptoh大学土木工程系开始使用,将此法移植到电磁场领域则是80年代的事。1978年以来曾召开多次边界元素法国际会议。应用前景是诱人的,但尚有许多不足之处:系数矩阵不是稀疏阵;矩阵中所有元素都要用数值积分计算;计算时间长;不适易处理多种介质问题;场区材料性质复杂。3.等效源法。是近10年来发展起来的求解静电磁场问题的有效方法,是将原边值问题化作电源问题来处理的,它把边界的影响,用虚设的模拟电荷的影响来等效代替。因此本质上也属于边界元法。4.矩量法(MOM)。是一种将连续方程离散化为代数方程组的方法,此法对于求解微分方程和积分方程均适用。格林顿(R.F.Horrington)于1968年出版的专著中。对用此法求解电磁场问题作了全面而深入的分析,用统一的观点简明扼要地介绍了这种方法。矩量法是先将所求方程写成带算符的符号方程,再将待求函数表示为某一组选用的基函数的线性组合,并代入符号方程,最后用一组选定的权函数对所得方程取矩量,得到一个代数方程组再求解。广义讲,它能统一各种数值方法,只是基函数和权函数取各种不同形式的结果。此法在天线分析和电磁场散射问题中有更广阔的前景。此外,还有几何绕射理论和时域电磁场的分析方法(高频近似方法);奇点展开法(SEM,1975年Prony提出)和时序法;时域差分法。因为各种计算方法各有优缺点,分别适用于各种不同的场合,所以,近年来提出了各种不同方法相结合的组合法。例如实验方法与解析法相结合;解析方法与数值方法相结合;各种不同的数值方法间的结合;有限元-边界元法;有限元-模拟电荷法;模拟电荷法一矩量法;区域变换-有限元法;奇点展开法与变分法;矩量法与几何绕射理论,格林函数法与矩量法等等。本课题今后的研究热点是:(1)完善这些方法,并应用到三维,非线性,时变的场合;(2)研究通用化的程序,即发展各种电磁场计算的软件包,以减少从事计算的人员编制程序的工作量,如输入数据的自动编制,输出数据的自动处理。用输入、输出数据的图像装置来进行控制。用小型计算机的处理都还将进一步发展。(3)计算精确度的明确化;(4)探讨另外新的计算方法,例如最小二乘配点法,蒙特卡罗法,网格图论法,伴随场法。(5)综合各种数值方法优点的组合法仍然是一个研究方向。【参考文献】:1 Roger F.Harrington.Field computation by Moment Methods,1981,62 Chari M V K,Silvester P P.finite elements in electrical and magnetic field problems,1985.33 河野照哉宅間董.电磁场数值计算法,1985.114 周省三,邵汉光.静态电磁场的数值计算,1987.85 李忠元.电磁场边界元素法,1984.126 樊明武,颜威利.电磁场积分方程法,1988.17 刘圣明.电磁场的数值方法,1991.48 盛剑霓.工程电磁场数值分析,1991.11(华北电力学院孙孝瑞副教授、陈斌发硕士撰) |

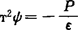 或T2ψ=0(偏微分方程)过去通常有两类方法:(1)严格解析法或称为解析法。经典方法有求解偏微分方程的分离变量法和求解积分方程的变换数学法——格林函数法。(2)近似解析法或称为近似法。在数理方法中,主要的有逐步逼近法、微扰法、变分法和迭代变分法。还有采用高频技术的几何光学法、物理光学法、几何绕射法(GTD)等以上解析法只能求解一些典型的问题。许多算法只适用于二维和稳态问题,不适用于不均匀和非线性问题,另外需花费一定的精力寻求特殊的算法和技巧。而实际电磁场的问题相当复杂。
或T2ψ=0(偏微分方程)过去通常有两类方法:(1)严格解析法或称为解析法。经典方法有求解偏微分方程的分离变量法和求解积分方程的变换数学法——格林函数法。(2)近似解析法或称为近似法。在数理方法中,主要的有逐步逼近法、微扰法、变分法和迭代变分法。还有采用高频技术的几何光学法、物理光学法、几何绕射法(GTD)等以上解析法只能求解一些典型的问题。许多算法只适用于二维和稳态问题,不适用于不均匀和非线性问题,另外需花费一定的精力寻求特殊的算法和技巧。而实际电磁场的问题相当复杂。