“奶牛标准产奶量校正系数”的概念、定义、翻译、参考文献-科学参考

单词

奶牛标准产奶量校正系数

释义

【奶牛标准产奶量校正系数】

拼译：correcting coefficient for standard milk production in dairy cow

在奶牛选种中需要正确地评定个体产奶量的遗传效应，排除各种非遗传效应的影响，其办法就是制定校正系数，利用校正系数将产犊年度、年龄、月份、胎次和泌乳天数等非遗传效应校正到同一水平，即估计校正产奶量(305d产乳脂率为4%的奶量)。

制定产奶量校正系数有两种方法。一种是针对个别因素分别制定出各种校正系数；另1种是对多种因素同时进行校正。在现有的研究报导中以第1种方法居多。无论哪一种校正方法，都是以准确地估计产奶量为前提，然后以确定条件下的奶量估计值为标准，求得校正系数。

关于时间与产奶量关系的数学模型研究报导较多。Gains(1927)首先利用数学模型描述了产奶量与时间的函数关系：

Y₁（）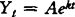

式中：Y_t是第t个时期的产奶量，e是自然对数的底，a、k是模型参数。

此后，新的数学模型不断推出，至1967年Wood提出不完全г函数模型：

Y₁（）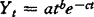

式中：Y_i为第t个泌乳阶段的平均日产奶量，a、b、c是模型参数。对于黑白花奶牛用产奶量的对数形式表示，该模型可以解释89．7%的总变异。许多学者就本国乳牛泌乳曲线进行研究后认为Wood氏模型较好。此后，有些学者对Wood氏模型进行了改进，提出不同的数学模型。如Cobby(1978)考虑了渐进因素，提出了如下模型：

　　　　Y_t=A(1－e^－qt)e^－kt　　　　(1)

　　　　Y_t=A－kt－Ae^－dt　　　　(2)

其中：A、d、q、k是参数。式(1)实际上是间隔模型，式(2)在高峰后趋于直线Y_t=A－kt。

Schaeffer(1977)在间隔模型基础上加上一个剩余项，其剩余结构为：

e¹=e^{r·t·sin(t．p)}

式中：r和p是参数，在一个胎次年龄组内是一个常数。用此模型模拟效果较好。

徐慧如等(1982)建立了以泌乳天数为自变量(x)，以各泌乳天数的平均产奶量为依变量(y)的二次多项式函数：

y=－169．9701+24．3076x－0．01809x²

用此式拟合北京市黑白花奶牛产奶量，其拟合度R²值可达0．999808。

周家荣(1986)提出了平稳自回归模型：

LnY_t=lnY_t^*+LnE_t+ε_t

式中Y_t^*是Wood氏模型的拟合部分，其拟合的剩余部分也被考虑为泌乳周t的函数。用此模型模拟的R²值在0．99左右。

关于产犊胎次、年龄、月份与产奶量的关系，徐慧如等(1982)提出的数学模型分别为：

　　　　y=4703．2864+948．7024x－94．6548x²　　　　　　　(3)

　　　　y=3148．7361+95．6594x-0．5959x²　　　　　　　　 (4)

　　　　y=5612+89．6563x－37．2106x²+2．5560x³　　 (5)

式(3)是胎次(x)与平均产奶量(y)的数学模型，其R²值为0．9830；式(4)是年龄(x)与平均产奶量(y)的数学模型，R²值为0．9082；式(5)是产犊月份与平均产奶量的数学模型，R²值为0．9113。

以上这些单一因素与产奶量关系的数学模型，虽然拟合度较高，但没有很好地考虑其它因素以及各因素之间的互作效应。陈德全等(1990)采用多元多项式回归分析方法，以产犊年度、月份、胎次和泌乳天数为自变量(xi)，以产奶量为依变量(y)建立了多元多项式模型，可估计多因素组合下的产奶量，其R²值达0．9592。在多元多项式模型中，既考虑了各因素的单独效应，也考虑了各因素之间的互作效应。

拟合度较高的各因素与产奶量关系的数学模型，是估计产奶量、制定校正系数的基础。制定校正系数一直沿用的传统方法是“单独逐项”校正。具体步骤是，首先根据单一因素与产奶量的函数关系式求得该因素各个取值的估计产奶量，然后确定该因素的标准取值，以各取值的估计产奶量除以标准取值的估计产奶量，求得校正系数，列出校正系数表。

陈德全等(1990)根据所建立的多元多项式模型，提出一种新的校正产奶量方法，即：

y_校=y_实－y_估+ŷ_标

式中：ŷ_校为某头牛的标准产奶量(即305天产奶量)；ŷ_实为某头牛实际产奶量；ŷ_估为根据多元多项式求得的产奶量；ŷ_标为规定各因素标准取值后利用多元多项式求得的产奶量。这种校正方法与校正系数表方法相比，能完整地保留产奶量这个性状的个体遗传效应值，校正结果逼近客观实际。

欲求得标准产奶量，除了用上述方法进行产奶量校正外，还需进行乳脂率的校正。关于乳脂率校正方面的研究报导较少，一直沿用的是Gaines(1928)提出的脂校正奶(FCM)方法，其计算公式为：

FCM(4%)=0．4M+15F

式中：M为奶产量，F为脂产量。

关于校正产奶量的研究，在有大量完整的现场数据和计算机的情况下，有必要采用和推广多种因素同时校正的方法，数理统计方法可采用多元多项式或最小二乘等方法。作为乳脂率这一指标如何进行合理的校正也是有待研究的课题。

【参考文献】：

1 Wood P D P．Nature，Lond，1967．164～216

2 Schaffer，L．R．，J．Dairy Sci．，1977，60：1636

3 Cobby，J．M．，Animal Prod．1978．26～27

4 徐慧如，张斌，王佳英．中国黑白花奶牛论文集，1982(11)：88～107

5 周荣家．国外畜牧学--草食家畜，1987(2)：19～20

6 望丕县．国外畜牧科技，1987(3)：14～15

7 陈德全，杨静华，庞为真，吉林农业大学学报，1990，12(1)：62～63

(吉林农业大学陈德全、杨静华撰)

随便看

科学参考收录了7804条科技类词条，基本涵盖了常见科技类参考文献及英语词汇的翻译，是科学学习和研究的有利工具。