【强极限理论】
拼译：strong limit theory
是以研究强逼近理论随机过程样本轨道性质及随机序列部分和增量渐近行为为主要对象的极限理论的一个重要方面，是自20世纪70年代以来概率论最活跃的分支之一。它包括研究Wiener过程及其相关Gauss过程的样本轨道渐近性质，并用它来逼近较一般的过程或随机序列，从而导出后者的样本轨道或增量的渐近性质，也包括直接研究更一般的过程的样本轨道性质，及较一般的随机序列的增量性质。
关于Wiener过程的重对数律(Lévy，1937)、钟开莱重对数律(1948)及独立同分布随机变量(i．i．d．r．v．)序列部分和的Hartman-Wintner重对数律(1941)等极限理论的经典定理是强极限理论的早期结果。Strassen(1964)强不变原理的出现开创了近代强极限理论研究的先河。至70年代，以匈牙利C
org ő．M和Révész．P等为代表，获得一系列结果，如关于Wiener过程增量理论，i．i．d．r．v．序列的部分和用Wiener过程的强逼近及其增量理论，经验过程及分位点过程用Brown桥及Kiefer过程的强逼近等等，它们组成了强极限理论的基本内容，被总结在Csörg ő和Révész的专著《Strong Approximations in Probabilityand Statistics》(1981)中，正如该书前言中指出的，今后将进一步开展(1)多参数部分和的强极限理论；(2)高维欧氏空间或Banach空间情形的强极限理论；(3)非独立情形；(4)独立非同分布情形强极限理论的研究。80年代强极限理论的发展是在不断深化原来已被研究的领域同时，在上述4个方面开展了卓有成效的工作。在这些研究中吸引了许多概率论学者参加，中国学者也作出了重要贡献，他们的主要结果已被总结在林正炎、陆传荣的专著《强极限定理》中。1．Wiener过程的增量理论。Lévy的连续模定理是Wiener过程｛W(t)，t≥0｝增量的早期结果，即
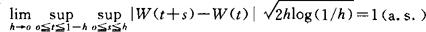
在它与重对数律基础上，Csörg ő和Révész提出了增量理论。首先讨论增量有多大，即证明
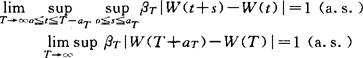
且T／aT也是不减的，βT=｛2aT(log(T／aT)+loglogT｝－1／2。当aT还满足(*)lim(log(T／aT))／loglogT=∞时，上面第1个式子中limsup可改为lim。以后国内外许多学者讨论当放宽条件(*)时，如何修改正则化因子使上述形式增量的下极限为1，也讨论了这类增量收敛的速度。从统计问题引出的增量的另一种形式－滞后增量有多大也被研究了，即
随后综合这两种形式还给出了增量的一般形式。此外，在钟重对数律基础上，Csörg ő和Révész讨论了Wiener过程增量有多小。这些结果还都被相应地推广到Wiener过程局部时的增量上。两参数Wiener过程｛W(s，t)，O≤s，t＜∞｝的增量也被深入地研究了。对于某些特殊选取的矩形集合LT，Csörgő和Révész证得
，其中δT是与LT有关的正则化因子，在一定条件下，limsup也可改为lim。国内一些作者把一参数情形许多结果推广到两参数情形，诸如相应下极限存在的条件，另一类重对数律，滞后增量，增量的一般形式，增量有多小等都被一一研究了。2．随机变量序列部分和的强逼近。Strassen利用Skorohod嵌入原理证明了第1个强逼近结果：
，其中Sn是均值为0，方差为1的i．i．d．r．v序列的部分和。这方面的最佳结果是由Koml os、Major和Tusn ady给出的，他们通过发展分位点变换法，证得：设在零的某邻域中矩母函数存在，则｜Sn－W(n)｜=O(logn)(a．s．)；如仅设p(＞2)阶矩存在，则｜Sn－W(n)｜=o(n1／p)(a．s．)。Sakhanenko考虑了独立但不必同分布随机变量序列，在对矩母函数附加一定条件后，证明这类序列的部分和可以用一列正态随机变量序列的部分和以一定的速度强逼近。Einmahl研究了多维独立随机向量序列的部分和用多维独立正态随机向量序列部分和逼近的结果。对于相依变量序列(如各种混合情形)部分和的强逼近，国内外有许多作者利用Skorohod嵌入方法作了细致讨论，在不超过4阶矩有限时有较佳结果。关于多参数的随机场也有类似结果。3．部分和的增量。由上两部分可写出i．i．d．r．v．部分和增量的各类结果，如当矩母函数在零的领域内存在时，对不减正整数列aN，在一定条件下，有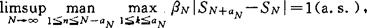
其中βN=｛2aN［1og(N／aN)+1oglogN］｝－1／2；当仅设p(＞2)阶矩存在时，也有同类结果成立。对滞后增量也有相应结果。又当aN～logN时成立着相应的大数律。
关于独立但不必同分布的随机变量序列，由于强逼近结果未达到同分布情形那样完美，故为给出相应结果需另辟途径。林正炎利用直接建立增量的尾概率精确估计，在一定的矩条件下，对Csörg ő-Révész增量、滞后增量及大数律都给出了理想的结果。此外，对没有矩假设的场合及一些相依变量情形，也建立了部分和增量结果。邵启满还研究了部分和增量有多小，不仅改正了Csörg ő-Révésy书中关于这一问题论证的不慎之处，而且推进到独立不同分布情形。4．经验过程。用Brown桥及用Kiefer过程的强逼近，作了相当完美的讨论，且被扩展到分位点过程(也称逆经验过程)上，并进一步利用这些来讨论经验过程、分位点过程本身的样本性质。5．Gauss过程的增量。作为Wiener过程增量的另一种拓广，近年来对于具有重要实际背景的无穷维Ornstein-Uhlenbeck过程有较多讨论。Csörg ő和林正炎讨论了它的样本轨道性质，包括连续模和重对数律等。随后，又被Csörg ő、林正炎和邵启满推进到更一般的lp值Guass过程上，讨论了它们的样本轨道性质。【参考文献】：1 Strassen V Z. Wahrasch. verw Gebiete,1964,3:2112 Komlos J, Major P, Tusnady D Z. Wahrsch. verw Gebie 111,1976I34I333 Csōrg ó m, Revesy p. Strong Approximations in Probability and Statistics:New York:Academic Press,19814 林正炎．中国科学，1984，27：10655 Chen G J，Kong F C，Lin Z Y．Ann Probab，1986，14：12526 邰启满，陆传荣．中国科学，1986，29：12437 林正炎．中国科学，1988，31：4678 Shao Q M．Ann．Probab．1989，17：8099 Csörg 6 M，Lin Z Y．Probab．Theory Rel，Fields，1991，89：42310 林正炎，陆传荣．强极限定理．北京：科学出版社，1992(杭州大学林正炎教授、陆传荣教授撰)