【方差组分估计】
属于数理统计学的一个主要内容。数量遗传学的遗传参数估测对于种畜鉴定乃至整个育种工程都极关键。要进行遗传参数估测，需进行方差组分估计。方差组分估计越准确，所得到的参数估值就越准确，这些参数应用所带来的结果——育种进展也就随之越大。方差组分估计虽然属检数理统计学的研究范畴，自20世纪30年代以来一直都是数量遗传学的一个热门研究课题。
1967年前，方差组分估计研究，进展较为缓慢。方差组分估计其实只有一条途径，便是令各平方和等于其相应的数学期望。这种办法最初见于Da—niels(1939)和Winsor与Clarke(1940)的研究。对于次级样本含量相等的均衡资料，这种方法中的各平方和即为传统的方差分析(ANOVA)中相应的平方和，其在一些模型下的具体应用可以见于Anderson与Bancroft(1952)的研究，而其最小方差特性则由Graybill等人于20世纪50年代后期和60年代初期导出，具体可以见于Graybill(1954)，Graybill与Wortham(1956)以及Graybill与Hultquist(1961)的研究。对于不平衡资料，即次级样本含量不相等甚至有的次级组数据缺失的资料，ANOVA无法使用，从而使得方差组分估计极其困难。在这方面，Henderson(1953)的研究可被看作一个里程碑。其中所提出的3种方法被人分别称为Hendersom法1、法2、法3。3种方法的估计量都是二次型、无偏估计量。法1只能用于随机模型，但是计算最为简单；法2可以用于混合模型，但是要求r(XZ)=r(X)+r(Z)－1(在此X、Z分别为模型中固定效应和随机效应的设计矩阵)，并且固定效应和随机效应之间不能存在互作，模型也不允许随机因素在固定因素内系统分组；法3可以用于混合模型且较法1、法2更为准确，但其结果不具有唯一性，且计算起来较为困难。这些方法曾在一段时间之内被人广泛推广，阐释以及应用(Searle，1971)。但是它们并未使使得方差组分估计技术有个根本性的飞跃，因为它们所采用的办法几乎完全同于均衡资料时的有关平方和，并令这些二次型等于其数学期望，它们的估计量也是除了无偏之外别无其它特异的统计特性。1967年，Hartley与Rao在正态分布的假设条件下给出的最大似然法(ML)使方差组分估计技术前进了一大步。这种方法具有5个特点：(1)估计量为有偏估计量；(2)假设观测值服从多维正态分布；(3)不具备平移不变的特性；(4)需通过迭代求解，但是计算相对较为简单；(5)估计量具有最大似然性。后Patterson与R．Thompson(1971)在W．A．Thompson(1962)的基础上，给出了另外一种最大似然法即约束最大似然法(REML)。这种方法同ML的区别在于它把估计固定效应所造成的自由度损失考虑了进去，因而其估计量具有平移不变的特性，但是这种方法的求解相对而言要复杂一些，另一方面，从Townsend(1968)及Townsend与Searle(1971)开始，人们的注意力开始集中于研究具有无偏和最小抽样方差的二次型估计量上。这导致了最小范数二次型无偏估计(MINQUE)法的问世(C．R．Rao，1970)。这种方法具有无偏、平移不变、在先验值的假设条件下最优(Euclideam范数最小)并对观测值的分布无所要求等特点。与此对应，1970年Lamotte在正态分布的前提下给出了局部最小方差二次型无偏估计法(MIVQUE)。这种方法要求观测值服从多维正态分布，且其最优是指估计量的方差最小，其它与MINQUE相同。除了ML、REML、MINQUE以及MIVQUE之外，尚有其它一些方差组分估计方法，如Harver(1970)的直接最小二乘法和Hemerson的新法等等。这些方法都充分地考虑到了估计量的抽样方差这一问题，而且大多也兼顾了无偏这一特性。但是如此多的方法使得面对一具体的非均衡资料究竟应采用哪种方法成了难题。20世纪80年代以来，人们对这些方法的应用及其间的关系开展了研究(Thompson，1982，1986；Meyer，1986)。另外，这些方法之间虽然稍微有所差别，但是对于现有的计算工具和计算技术而言都显得相当困难，因此这些年来人们也对计算方法作了一些探索。方差组分估计虽然已有多种方法，但是这些方法所依据的却都是线性模型。这种模型一般可以写为
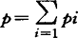；z是Nxq的已知设计矩阵，u为qx1的随机效应矩阵，二者可以剖分成为Z=［z1、z2…zs］和［u’1u’2u’s］，s是随机因素数目，若令ui为qix1矩阵，则
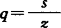qi；e为Nx1的随机误差矩阵；E(YUe)是各随机变量的期望矩阵；V(YUe)是模型中的随机变量的方差与协方差矩阵；G与R分别为U的和e的方差与协方差矩阵，通常假定G=
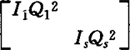R=IQe2，因此V=ZGZ+R=SziZiZiQi2+IQe2。可以看出，这个模型是很简单的。这意味着对下列问题有待于进一步的研究：(1)种畜之间存在亲缘关系，致使G为非对角阵的资料的分析；(2)多性状且这些性状间存在遗传相关时的分析；(3)误差方差不同质、即R≠IQGe2时的分析；(4)多个性状，而且这些性状分属连续与不连续两种，其分布类型有的一先所知；(5)选择下的资料利用。除了这些问题之外，次级组含量过少时的估计以及计算过程的简化也有待于进一步的研究。【参考文献】：1 Barker J S F，et al．Future developments in the genetic improvement of animals．Academic Press，1982，139～1552 Rao C R．Estimation of variance and covariance components-MINQUE．theory．J．of Mulivariate Analysis，1971，1：257～2753 Hartley H O，et al．Maximum likelihoodestimation for the mixed analysis of Variamce model．Biometrika，1967，54：93～1084 Patterson H D，et al．Maximum likelihood estimation of variance components．Proceedings of the 8th International Biometric Coinferene，1974，197～207(东北农学院潘玉春博士撰；盛志廉审)