【马太分析】
拼译：Meta-analysis
1977年美国格拉斯、(G．V．Glass)首先提出马太分析，他在《教育研究展望》上发表了《综合研究成果：研究的马太分析》。马太分析使研究一体化，是可用于各单项实验综合分析资料的一种定量手段。通过记录各分散研究的特性和以定量表达的成果，把各种形形色色的、经统计检验有充分信度的各种成果一体化。因此，马太分析实际上是使用多种测量手段和统计分析的一种正确观测事物相互关系的方法。其目的是在某种研究领域中，基于已发表的大量研究资料，通过马太分析综合成具有普遍意义的结论。
在体育科学中所以引入这种方法，缘因于当前体育研究中日渐暴露的诸多问题。如研究成果的传布：演示及评价手段缺乏系统的体系；需要研究的问题不明确，不知道什么样的研究需不需要进行；知识爆炸和学术期刊的激增；体育领域中各分学科一体化的发展缺乏手段；研究者与实践者之间信息交流的滥用，不足乃至全无；现有的学术奖酬体制中未能体现出综合应用的协调活动；缺乏把研究成果的潜在利益以有效手段推广到应用者手中的市场机制。当前与体育有关的研究文献以几何级数在增加，虽然它具有积极的一面，可使人们得到越来越多的信息。同时它又存在消极的一面，因为研究意味着要对无组织和无关的点点滴滴的信息或高度抽象的理论从现实经验中迁移出来。1977年利(K．L．Ley)指出：“以各种思想和概念体现出的新知识，其发展速度之快，远超过我们能设法应用它的速度……”。况且对诸如运动心理、运动生理、生物力学等的研究，经常产生相互矛盾的结果。对于这些研究成果相一致或矛盾的大量信息，因缺乏使它们相互联系、再分析和解释它们的方法而处于“冰冻”状态。在体育的某些领域中的研究，由于受作业、受试者、环境及研究设计等无法估计到的多变性因素的影响，致使研究结果不稳定。即使是研究条件能较精确地控制的某些领域，如运动生理的研究，所得结果也会大相径庭。马太分析的基本思想是使无序状态下的大量信息变成有条不紊。它与传统的文献回顾不同，首先是马太分析为文献回顾的决断过程提供了一组程序，而传统上的回顾与分析有较大的偶然性。其次，文献回顾一般只对研究结论作定性分析，而马太分析却对研究成果进行再加工的定量检验分析。1986年托马斯(J．R．Thomas)列出作马太分析的步聚：(1)明确研究分析的问题。(2)文献探索、包括电脑探索，期刊索引和学位论文与文献综述。(3)精读每一个研究，对实验特征进行编码。(4)对研究结果作定量分析，计算其效应值(Effect Sizes)。(5)对各研究的效应值作统计分析。(6)结果解释。(7)以述评报导分析结果。从概念上看，马太分析是把某种研究成果转换成定量数据，称为效应值。它表示了对实验处理效应的一种常规量度。1977年格拉斯把效应值定义为：实验组的均值和对照组均值之差除以对照标准差。其定义公式：ES=(Mr－Mc)／Sc，式中Mr为实验组均值，Mc为对照组均值，Sc为对照组标准。用此公式，可把某一研究中的一种结果转换成标准单位，以便于解释。例如效应值0．68，可解释为实验组的一名受试者的因变量上的得分比对照组的一名受试者的因变量上的得分高出三分之二的标准差。因此，效应值的代数符号非常重要，它表示了是实验组抑或对照组的因变量的成绩好坏。研究遇变量越小成绩越好时，定义式中的MrMc要改成Mc－Mr，使正的效应值代表正的实验处理效应。当所检索到的文献未报导平均值和标准差时，有些学者(如G．V．Glass，M．L．Smith和L．V．Hedges等人)提出用其它统计量来估价效应值的方法：(1)若已知T检验的T值，则ES=T(l／N，+l／Nc)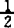
。(2)若已知F检验的F值，则ES=2(F／(NTNc))
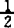。(3)若已算出标准变量，即
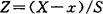，则ES=ZrZc。(4)也可以对T检验作修正，则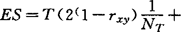
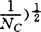应用马太分析作的早期研究多数用参数方法计算效应值，但是赫奇思(L．V．Hedges)等近几年对马太分析进行深入研究后指出，用参数方法并非是分析研究成果效应值的最佳方式。他们对格拉斯的马太分析的有效性提出了质疑。其中主要的批评是：它以不同的测量量表、方法和实验设计和得来的各种成果予以混合。对于那些研究中的内部效度和方法学上的控制能清楚地表明存在明显的差异，而用格氏分析法只显示出微小的差异。赫氏等人引伸并发展了格氏的初始成果，提出了专门设计的统计检验方法。这套新的检验方法是针对过去马太分析中存在的问题而加以改进的，它主要包括下列6方面的内容：(1)计算效应时，应以什么指标作标准差?(2)鉴于样本效应值是总体效应值的偏估，如何修正?(3)由于样本容量不同，样本效应值是否要加权?(4)一个样本中的所有效应值是否来自同一总体，即样本效应值是否具有同质性?(5)效应值的适宜的统计检验方法是什么?(6)在样本效应值中杂有异常数据能否检验出来?赫氏对解决这些问题所持的理论依据可概述成：为效应值选择标准差的问题。赫氏认为方差的合并估计值才是总体方差更精确的估价值，它的优点是增加了与方差估价相关联的自由度。Sp=((NT－1)Sr+(Nc－1)Sc)／(NT+Nc－2)，这里，NT和NC分别为实验组和对照组的样本容量，Sr和Sc分别为两组的方差。计算效应值的标准差即是加权合并方差的平方根(
)。因各组方差是异质时(在称名变量的效应检验中是常见的)，算出的效应值是偏估的。而参数检验是以等方差假设为条件的。赫氏为使用效应值作为处理效应的估计量提出一种理论和结构模型，他认为单个效应值可作为估价总体存在的处理效应的样本统计量，即效应值方差=(NT+Nc)／(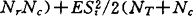
)。赫氏证实了小样本中的效应肯定是偏估的，可通过下式求出修正系数：C=1－(3／(4m－1))，式中m为自由度，它随所取的标准差不同而异。关於样本容量对效应值加权问题，赫氏认为通过效应值方差的倒数给每一个效应值加权。效应值方差越小说明估价值越准。它在计算总平均值时予以更大的权重，使加权平均值在估价总处理效应时会更精确。关于样本效应值的同质性检验问题：早期的马太分析是没有显著性检验的。赫氏分别于1982年和1983年先后提出两种检验方法：第一种是把检验统计量H值分割成效应值的组间平方和HB与组内平方和Hw，均以方卡(X2)作准则检验；另一种方法是用加权回归方程。有两篇论文(D．L．Feltz，1983；J．R．thomas，1985)所作的4个马太分析使用的是加权回归方法。影响效应值的研究特征常常不止一个，尤其在效应值数量很多时更如此，而用回归方程作马太分析时可以容纳更多变量而不会增高统计检验的α水平。关于检验异常数据的问题，1985年赫氏是通过回归方程中的残差项检验来鉴别异常数据的。因为残差的绝对值可以转换标准化变量Z，当标准化了的残差效应值大于2时，就可将其作为异常数据来考虑。马太分析在实践中尚存在一些问题，即当研究报告中没有计算效应的全部信息时，某些学者提出从其它统计量来估价效应值的方法。但碰到两组没有显著差异的报导时，托马斯用零效应值来替代，但在同一个马太分析中取太多的零效应值又可能产生同质的假象。为此，赫氏主张用修正系数来调节。迄今还未发现有一种理想的方法来解决这一问题，在中国的体育文献中，至今未发现用马太分析作综合研究报导。在1990年北京亚运会科学报告会上，南朝鲜学者康桑安(Kang Sang-Jo)曾作过“肌肉力量的性别差异——马太分析”的报告。【参考文献】：1 Glass G V．Review of Research in Education，1977，5：351～3792 Sparling P B．Research Quarterly for Exercise and Sport，1980，5l：542～5523 Hedges L V．Journal of Educational Statistics，1981，6：107～1284 Thomas J R，et al．Psychological Bulletin，1985，98：260～1285 Rothstein S L．Researh，design & Statistics for Physical education，Prentice-Hall，Inc．，1985．216～255(华南师范大学陈骏良教授撰)