【算子逼近】
拼译：operator approximate JN．
渊源于积分方程的核用退化核逼近所产生，乃提出一个有界线性算子T∈B(X，Y)被紧算子或有限秩算子最佳逼近。最先有1960年GohbertKrein及Schatten的书详细研究了Hilbert空间中的紧算子集K(H)。建立由特征值导出的S－数一套理论
则
‖A－T‖=Sn+1(A)．A∈B(H)则
，且有T0到达inf。1970年N．Các证明当X，Y自反，Y具收缩基底，则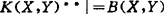
。
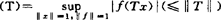。1985年C．S．CardasS继续深入，1982年I．D．Berg和B．Sims证出对匀凸X，NRA(X)稠于B(X)。1987年他们又证X可以是c0，l1，L(μ)光滑空间等。1989M．Acosta和R．Polya证出凡B．空间二次共轭是NRA的空间(
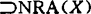)总是调于B(X)的。C．W．Kim1975～1980年研究了收缩算子集的可逼近性。主流仍然是研究K(X，Y)在B(X，Y)中的可(逼)近性为最大课题。首先由于一般B(X)不是自反，又只要dimX≥2则B(X)又不是严凸的，所以难指望空间几何理论去解决之。是否X，Y施加良好条件，即达到可近性呢?1971年Holmes和Kripke已指出即使是Hilbert空间，Y匀凸，仍然出现K(X，Y)不可近(指在B(X，Y)中不可近，以下都略去此句)，故更多讨论到X=Lp(μ)情形，或Y=C(Q)情形。Holmes氏就一般X，Y推出过
与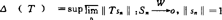
的一个关系△(T)≤δ(T)，且若存在T0全连续，‖T－T0‖≤ΔT则T0必是T的佳逼全连续算子。‖T－T0‖=Δ(T)=δ(T)。特别就H1，H2空间就存在T0。实例算子空间解决全连续佳逼的第一个范例为1978年Mach和Ward证出K(l1)是可近集。且
这里(ti，j)是T的表现矩阵。1980年M．Feder更考虑T：l1→L1(μ)则K(l1，L1(μ))可近的本征是μ是纯原子。1979年H，Fakhoury研究K(L1，Y)可近性，是运用Y中有界集B的非紧度α(B)为工具建立了F，氏公式d(T，K(X，Y))≥a(TUB)。由于T可表现为
，表现子x(5)∈L∞(μ，Y)的T像集叫B，故此予设Y匀凸时，K(L1(μ)，Y)是可近的，且T到它的佳逼度为α(B)。刚才Y不设匀凸却大不同。1980年Feder首先发现K(L1［0，1］)为不可近集。K(C［0，1］)也不可近。这就说虽X可分，而K(X)可以是不可近集。1985年Y．Benyamini和P．K．Lin研究了K(Lp)，K(Lp，lp)，K(lp，Lp)等，分别1＜p＜2，2＜p＜∞，其中T∈B(Lp)，2＜p＜∞，若合Weis条件即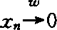
，xn匀囿。则‖Txm‖→0，则T有佳逼紧算子。另一大类算子空间K(X，C(Q))的可近性研究颇多。最重要是J．Mach1978年创立X的M1与M2条件，谓X*中凡有界网(xa)及y∈X*，‖xa+y‖与‖xa｜｜之差趋于‖y‖，而是按某种权函数意义而言。若X合M1条件，则K(X，C(Q))是可近集。除了Hibert空间；lp(1＜p＜∞)，c0都合M1条件。若减弱为X只合M2条件则无可近性结论，但每个T∈B(X，C(Q))可估出佳逼度下界
，u是T的表现子。1980年K．S．Lau独立考虑了X匀光滑得到K(X，c(Ω))(Ω是拓扑空间)是可近集。联系到K(C［0，1］)的不可近性，自然要问K(C(Q))有何种Q使它可近吗?要求Q的本征问题到1989年Yost基本有了部分回答。有限秩算子集(秩≤n)Kn(X，Y)的可近性方面，最早已证Kn(H)可近性。但似乎太难发现不可近的例。直至1986年Kamel又有例子Kn(l1，c0(S)及Kn(l1，C(Q))，而紧集Q设含正整数集一点紧化同胚像Q，它们在相应全连续算子空间中不可近。可注意的是Kn(l1，c0)不可近于B(l1，c0)，而K．Saatkamp早些证出K(l1，c0)可近。Kamel建立了一个“缩像原理”：若Kn(X，Z)可近，Y是Z中范数1余子空间，则Kn(X，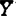
)可近。关于Kn(X，
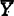)于K(X，
)不可近例还同时发现(X，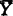
)为(co，c)，(c，c)或c0(S)都是。Kamel解决另一问题是KN(X，
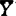)可近，是否导致任n，Kn(X，
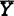)可近呢?即N是否本质固定或否呢?他予以否定回答。事实上，任m≠n有某有限维X，紧HausdorffQ使Km(X，C(Q))可近而Kn(X，C(Q))不可近。1972年E．M．Alfsen和E．G．Effros阐述了M－伊(ideal)，Lp和块(summand)等类特殊投影子空间的结构。追溯最早1950年J．Dixmier已证出K(H)是B(H)中的M－伊。当时尚未以M－伊命名。由于著名三球定理的建立，大大显露了M－伊构造才广泛用到实例空间中。例如1971年T．Ando证明了M－伊是可近集及合Pheps氏(U)唯一展拓性。1975年P．Smith J．Ward证出K(l1)非M伊却可近。A．Lima1977～1979三年卓著工作中建立三单位球定理及引入半M－伊，他证出凡M伊上的度量投影PM总是Lip的dH(Pmx，Pmy)≤2‖x－y‖，且PM恒有连续选。他又最先证出c0是l∞中的M伊。1979年Lima大量地证出K(lp，lr)1＜p≤r＜∞是M伊，而K(l1)，K(l1，lp)，K(lp，l∞)，K(c0，l∞)都非M伊，但却可近。随后又证出K(l∞，l∞)不是可近集。较早些1973年J．A．Hennefeld已证K(c0，c)，K(lp，co)(1＜p＜∞)是M伊。1979年Yost与1978年Smith和Ward都独立证出K(X，c0)是个M伊。1980年Saatkamp证K(X，c0(s))恒是个M－伊。Lima又研究Y是Lindenstrass空间，则K(lp，Y)(1＜p＜∞)，K(C0(T)，Y)都是M－伊。1985年C．Cho W．Johnson研究闭子空间
何特征使K(X)是M伊。1979年Yost引入子空间M的
球性，乃三球性中一球指定了是单位闭球。所以它是M－伊的弱化。仍获得凡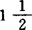
球性子空间是可近集，Pm恒有拟加，齐性单值选。Yost发现一有趣事实，在复域下K(c，c)不具
球性，但实域下却具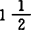
球性。K(c0，C(Q))实域下亦如此，复域下则仍未证实属谁。不过K(c0，c)却不同，它在实复域下都具
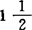球性。Yost又引入三球性又一种弱化条件。叫Yost性。上述关于M伊、半伊、
球性、Yost性这些子空间已探明实质确有区别，不过实例验明则远远未全清楚。【参考文献】：1 Halmos PR. Indiana Univ M J, 1972,21(10):951～9602 Alfsen E M, Effros E G. Sturcture in real Banach spaces An M,1972.96:98～1733 FederM. JAT,1980,29:170～1774 MachJ. Pro AMS, 1978,72(1): 99～1045 潘文熙．全国第3届泛函分析会议报告，1983：1～156 Kamal A. JAT, 1986,47:132～1717 Yost DT. JAT,1987,49:99～109.8 Bang H, Odell E. JAT, 1987;51:274～2879 YostDT. JAT,1989, 50:100～110(暨南大学潘文熙教授撰)