A connected graph with no cycles. A disconnected graph with no cycles is called a forest. It can be shown that a connected simple graph with n vertices is a tree if and only if it has n − 1 edges. The figure shows all the trees with up to five vertices (see Cayley’s Theorem).
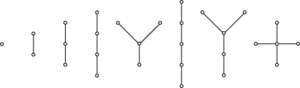
Trees with five vertices or fewer
Particularly in applications, one of the vertices of a tree may be designated as the root, and the tree may be drawn with the vertices at different levels indicating their distance from the root. A rooted tree in which every vertex (except the root, of degree 2) has degree either 1 or 3, as shown below, is called a binary tree.
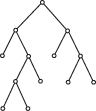
A rooted, binary tree
1. Most commonly, short for rooted tree, i.e. a finite set of one or more nodes such that firstly there is a single designated node called the root and secondly the remaining nodes are partitioned into n≥0 disjoint sets, T1, T2,…, Tn, where each of these sets is itself a tree. The sets T1, T2,…, Tn are called subtrees of the root. If the order of these subtrees is significant, the tree is called an ordered tree, otherwise it is sometimes called an unordered tree.
A tree corresponds to a graph with the root node matching a vertex connected by (directed) arcs to the vertices, which match the root nodes of each of its subtrees. An alternative definition of a (directed) tree can thus be given in terms from graph theory: a tree is a directed acyclic graph such that firstly there is a unique vertex, which no arcs enter, called the root, secondly every other vertex has exactly one arc entering it, and thirdly there is a unique path from the root to any vertex. The diagram shows different representations of a tree.
2. Any connected acyclic graph.
3. Any data structure representing a tree (def. 1 or 2). For example, a rooted tree can be represented as a pointer to the representation of the root node. A representation of a node would contain pointers to the subtrees of the node as well as the data associated with the node itself. Because the number of subtrees of a node may vary, it is common practice to use a binary-tree representation.
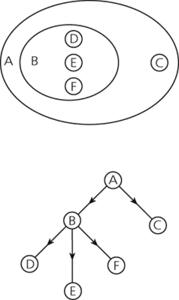
Tree. Sample tree represented as a Venn diagram (top) and as a directed graph
The terminology associated with trees is either of a botanic nature, as with forest, leaf, root, or is genealogical, as with ancestor, descendant, child, parent, sibling. See also binary tree.
- addition(of vectors)
- addition polymerization
- addition reaction
- addition rule
- additive
- additive function
- additive group
- additive identity
- additive inverse
- additive model
- additive primary colours
- additive process
- additive synthesis
- Addled Parliament (5 April–7 June 1614)
- add-on
- add-on manager
- add-on virus
- address
- addressability((of a display device))
- addressable location
- address book
- address bus
- address calculation sorting
- address format
- address harvester