A test for equality of two or more population variances. Suppose the sample variance for the jth sample is s_j² based on ν_j degrees of freedom. In the case of samples from two populations having normal distributions, the F-test compares the ratio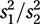with the critical values of an F-distribution with ν₁ and ν₂ degrees of freedom. The F-test is encountered most frequently in the context of an analysis of variance table (see anova), where it is often referred to as a variance-ratio test.

To test the hypothesis that m normal populations have the same variance, the Bartlett test (suggested by Bartlett in 1937) has test statistic (see hypothesis test), B, defined by: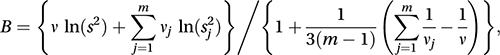where ν=ν₁+ν₂+⋯+ν_m and . If the null hypothesis of equal variance is correct, then B has a chi-squared distribution with (m−1) degrees of freedom.

Alternatives in cases where the sample sizes are equal are the Cochran C test, introduced by Cochran in 1941, and the Hartley test introduced by Hartley in 1950. The Cochran test statistic, C, is given by

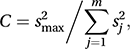
and the Hartley test statistic, H, is given by

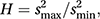
where s²_max and s²_min are, respectively, the maximum and the minimum of s²₁, s²₂,…, s²_m. Unusually high values of C or H indicate unequal variances.

All of these tests are sensitive to departures from normality. See also test for equality of scale.