In its most general form, a tessellation is a covering of the plane with non-overlapping shapes. Often the shapes are polygons and the pattern is in some sense repetitive. A tessellation is regular if it consists of congruent regular polygons. There are just the three possibilities shown here: the polygon is either an equilateral triangle, a square, or a regular hexagon.

Tessellation with equilateral triangles
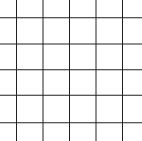
Tessellation with squares
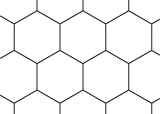
Tessellation with regular hexagons
A tessellation is semi-regular if it consists of regular polygons, not all congruent. It can be shown that there are just eight of these, one of which has two forms that are mirror-images of each other. They use triangles, squares, hexagons, octagons, and dodecagons. For example, one consisting of octagons and squares and another consisting of hexagons and triangles are shown here:
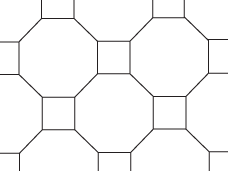
Tessellation with octagons and squares
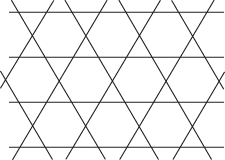
Tessellation with triangles and hexagons
Regular pentagons cannot tessellate the Euclidean plane (see Euclidean space). There are currently 15 known ways to tessellate the plane with congruent pentagons, the latest being found in 2015. Tesselations of the sphere and hyperbolic plane are also studied, where regular pentagonal tessellations do exist.
See also Penrose tilings.
A complete covering of a plane using a limited number of different shapes. Usually the shapes are polygons (as in the Dirichlet tessellation). The plane can be tessellated with rectangles, or hexagons, or triangles (for example, using Delaunay triangles). In a regular tessellation all the shapes are regular polygons (i.e. with all sides equal and all angles equal) of the same shape and size, and there are only three possible regular tessellations, using squares, equilateral triangles, or regular hexagons. Other semi-regular tessellations use two or more regular polygonal shapes, for example, squares and octagons. Many tessellations are periodic, i.e. the pattern repeats at regular intervals. A non-periodic tessellation, using two basic shapes, was invented by Sir Roger Penrose and is usually referred to as Penrose tiling.
A complete covering of the Euclidean plane by nonoverlapping regions.
- legacy applications
- legacy networks
- legal disclaimer
- legal geography
- legalism
- legal positivism
- legal realism
- legal tender
- Legendre, Adrien-Marie (1752–1833)
- Legendre, Adrien‐Marie (1752–1833)
- Legendre polynomials
- Legendre symbol
- Legendre’s conjecture
- Legendre’s differential equation
- legged robots
- Leggett–Garg inequality
- Leggett’s theorem
- legion
- legume
- Leguía, Augusto Bernardino (1863–1932)
- Lehmann, Erich Leo (1917–2009)
- Lehmann, Inge
- Lehmann, Inge (1888–1993)
- Lehmann, Johann Gottlob (1719–67)
- Lehmann–Scheffé theorem