Independent random samples are taken from populations with cumulative distribution functions F₁ and F₂. It is assumed that, for some constant δ, F₁(x)=F₂ (x+δ) for all x. The null hypothesis is that δ=0, corresponding to the case where the samples have been drawn from a single population (or two populations with the same distribution). The alternative hypothesis is that δ ≠ 0, which corresponds to the case where one distribution has slipped relative to the other. This sort of test is called a slippage test; the most common example is the Mann–Whitney test.

The matched-pair Wilcoxon signed-rank test requires the distributions under comparison to be symmetric. The Van der Waerden test is suitable for the comparison of continuous distributions. For samples of size m and n, the test statistic (see hypothesis test) of the Mood median test is the number of observations in a sample that are greater than the median of the combined set of data. The Savage test, which is suited to comparing skewed distributions, particularly the exponential distribution, uses as its test statistic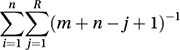where R₁, R₂,⋯, R_n are the ranks of the sample of size n when the two samples are combined and jointly ordered. See also test for equality of mean.