A matrix that captures the evolution of the age distribution of the females in a population. The female population is divided into g age-groups, each of width k years. The probability that a female, in group j at time t, will be alive in group (j+1) at time (t+k) is denoted by Sj. The mean number of female offspring born to a mother in group j between times t and (t+k), and alive at time (t+k), is denoted by Mj. The Leslie matrix, L, is given by
 The entries in this matrix are the mean numbers at time (t+k) resulting from single individuals in each group at time t. If N(t) is the g×1 column vector with entries being the mean numbers of females in the groups at time t then the Leslie model states that
The entries in this matrix are the mean numbers at time (t+k) resulting from single individuals in each group at time t. If N(t) is the g×1 column vector with entries being the mean numbers of females in the groups at time t then the Leslie model states that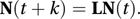
- methyl bromide
- methyl chloride
- methyl cyanide
- methylene
- methylene blue
- methylene chloride
- methylenedioxymethamphetamine
- methyl ethanoate
- methyl ethyl ketone
- methyl group
- methylidyne
- methyl methacrylate
- methylome
- methyl orange
- methylphenols
- methyl red
- methyl violet
- methylxanthines
- Metis
- Metius, Jacobus
- metocean data
- metol
- Meton
- Metonic cycle
- MetOp