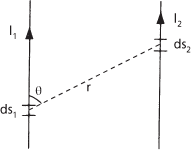
1. (Ampere–Laplace law) The force between two parallel current-carrying conductors in free space is given by
where I1 and I2 are the currents, ds1 and ds2 the incremental lengths, r the distance between the incremental lengths and θ the angle (see diagram); μ0 is the permeability of free space. Ampere’s law thus relates electrical and mechanical phenomena. See also Coulomb’s law.
2. (Ampere’s circuital theorem) The work done in traversing a closed circuit that encloses a current I is given by
where μ0 is the permeability of free space, B is the magnetic flux density, and ds an incremental length.
The total current flowing is given by the integral of the current density flowing in the area bounded by the loop. In a medium of magnetization M, the total current density, jT, is given by the sum of the real current density, j, and the equivalent magnetization current density, jM, where
Since
where dA is an increment of area, then
and thus
Since H, the magnetic field strength, is defined by
Ampere’s law, in differential form, may be written as
Ampere’s law
- double exponential distribution
- double factorial
- double fertilization
- double helix
- double image
- double integral
- double layer
- double-length arithmetic
- double-lined binary
- double-mindedness
- double-mode variable
- double modulation
- double negation
- double negation translation
- double planation
- double point
- double-pole switch
- double post
- double precision
- double pulsar
- double quasar
- double recessive
- double refraction
- double root
- double salt