When a population contains easily recognizable subpopulations, or strata, of known sizes (N₁, N₂,…, N_s), the method of stratified sampling will usually give better results than a simple random sample from the whole population. With stratified sampling, simple random samples (of sizes n₁, n₂,…, n_s) are taken from each stratum. The method was introduced by Neyman in 1934.

With proportional allocation the sizes of these samples satisfy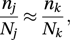for all j and k.

If the standard deviations of the values of the items in the various strata are known to be σ₁, σ₂,…, σ_s, then for a fixed sample size of n items, the optimum allocation (Neyman allocation) is obtained by choosing n_j so thatThis allocation minimizes the variance of the estimator of the overall population mean. If the standard deviations are not known then a pilot study can be used to obtain estimates of their values.