Let f be a continuous function on [a,b] and differentiable on (a,b), such that f(a) = f(b). Then there exists c with a<c<b such that f′(c)=0.

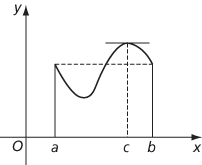
Two stationary points in (a,b)

The theorem is a special case of the mean value theorem. A rigorous proof relies on a continuous function on a closed, bounded interval attaining its bounds (Weierstrass’ Theorem).