A theorem, given by Cochran in 1934, concerning sums of chi-squared variables. Let Y be an n×1 vector of independent standard normal variables (see normal distribution) and let A1, A2,…, Ak be non-zero symmetric matrices such that
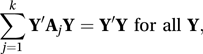 where Y′ is the transpose of Y. Write Qj=Y′AjY. Cochran's theorem, published in 1934, states that, if any one of the following three conditions is true, then so are the other two:
where Y′ is the transpose of Y. Write Qj=Y′AjY. Cochran's theorem, published in 1934, states that, if any one of the following three conditions is true, then so are the other two:(i) The ranks of A1, A2,…, Ak sum to n.
(ii) Each of Q1, Q2,…, Qk has a chi-squared distribution.
(iii) Each of Q1, Q2,…, Qk is independent of all the others.
- unsecured loan
- unshielded twisted pair
- unshielded twisted pair cable
- unsigned
- unskilled work
- unsolvable
- unsorted biosparite
- unstable
- unstable equilibrium
- unstable oscillation
- unsteady flow
- unsteady state
- unsterilized intervention
- unstructured model
- unstructured packing
- unsubscribe
- unsupervised learning
- Unsöld’s theorem
- untied aid
- unwind
- unzip
- UOD
- UP
- up
- Upanishads