A measure of the linear dependence of one numerical random variable on another. The phrase ‘coefficient of correlation’ was apparently originated by Edgeworth in 1892. It is usually denoted by ρ (rho). The value of ρ, which lies between −1 and 1, inclusive, is defined as the ratio of the covariance to the square root of the product of the variances of the marginal distributions (see bivariate distribution) of the individual variables: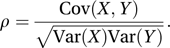If the correlation coefficient between the random variables X and Y is equal to 1 or −1 then this implies that Y=a+bX, where a and b are constants. If b is positive then ρ=1 and if b is negative then ρ=−1. The converse statements are also true.

If X and Y are completely unrelated (i.e. are independent) then ρ=0. If ρ=0 then X and Y are said to be uncorrelated variables. However, ρ is concerned only with linear relationships, and the fact that ρ=0 does not imply that X and Y are independent.