“Pascal’s theorem”的概念、定义、翻译、参考文献-科学参考

Pascal’s theorem

Mathematics

单词	Pascal’s theorem
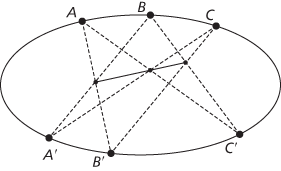
释义	Pascal’s theorem Mathematics A theorem of projective geometry: given two triples of points A,B,C and A′,B′,C′ on a non-degenerate conic, the points of intersection $A B ″ \cap B A', B C ″ \cap C B', A C ″ \cap C A',$ are collinear. Pappus’ Hexagon Theorem can be seen as a version of Pascal’s theorem for degenerate conics. Pascal’s ‘mystic hexagram’ The dual of Pascal’s theorem is Brianchon’s theorem: if a hexagon with vertices P₁, P₂, P₃, P₄, P₅, P₆ circumscribes a non-degenerate conic, then the hexagon’s diagonals P₁P₄, P₂P₅, P₃P₆ are concurrent. See duality.
随便看	congruence(modulo n) congruence relation congruent dissolution congruent figures congruential congruential generator method congruent solution Coniacian conic conical intersection conical pendulum conical scanning conic section conidiospore conidium Coniferales Coniferophyta Coniferopsida coniferous forest conifers conjectural variation conjecture conjugacy class conjugate conjugate acid or base