In a medium such as a semiconductor containing fixed charges and mobile charges, the distance required for a significant change in mobile carrier population under equilibrium conditions; the neutral equilibrium values of charge carrier density are either increased or reduced. The Debye length is a result of the screening effect around a fixed charge such as a donor impurity due to electrostatic attraction between it and the mobile carriers, causing them to cluster around the site of the impurity ion and mask its presence. Hence the electric field surrounding the ion declines much more rapidly than it would in the case of the unscreened ion. Fig. a illustrates the concept of Debye length for a positive ion. The ion has a charge +q and is surrounded by a cloud of mobile carriers – electrons in this case. The cloud is about a Debye length in radius and contains an integrated charge of –q.

In the case of a semiconductor where both electrons and holes are present, the general form for the Debye length is given by

where k is the Boltzmann constant, T the thermodynamic temperature, ε the permittivity of the material, q the value of the fixed charges, and n₀ and p₀ the neutral equilibrium numbers of electrons and holes respectively.

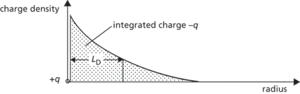
(a) Debye length for an ion, charge +q

From this, in an extrinsic semiconductor where the charge carriers are predominantly due to the presence of impurities an approximate value can be derived as

for n-type material, where N_D and N_A are the numbers of donor and acceptor impurities respectively.

For intrinsic material the value is

where n_i is the intrinsic carrier density for one type of carrier.

The Debye length can be used as a scaling factor to derive a curve that describes the manner in which the carrier density changes from its neutral equilibrium value to near zero, for example at the edge of a depletion region, and hence is a measure of the departure in practice from the sharp edge to the depletion region that is often assumed (Fig. b).

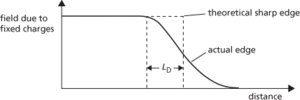
(b) Debye length, depletion region