The return of all or part of a beam of particles or waves when it encounters the boundary between two media. The laws of reflection state: (1) that the incident ray, the reflected ray, and the normal to the reflecting interface at the point of incidence are all in the same plane; (2) that the angle of incidence equals the angle of reflection. See also mirror; reflectance; total internal reflection.
Let l be a line in the plane. Then the mirror-image of a point P is the point P′ such that PP′ is perpendicular to l and l cuts PP′ at its midpoint.
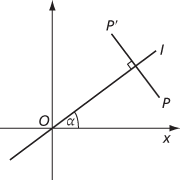
Reflection in l
Reflection in the line l is the transformation of the plane that maps each point P to its mirror-image P′. Suppose that the line l passes through the origin O and makes an angle α with the x-axis. If P has polar coordinates (r,θ), its mirror-image P′ has polar coordinates (r,2α − θ). In terms of Cartesian coordinates, reflection in the line l maps P with coordinates (x,y) to P′ with coordinates (x′,y′), where
In 3-dimensional space, an orthogonal matrix with determinant –1 and trace 1 represents a reflection in a plane containing the origin.
In higher dimensions, in ℝn, reflection in the hyperplane with equation r∙n = c is given by
If c = 0, this is represented by an orthogonal matrix. In general, reflections are isometries.
The rebounding of an object or wave (light, heat, sound, seismic, etc.) from a surface; the object or wave so reflected. In geophysics, a signal reflected from a reflector according to Snell’s law. A seismic reflection occurs as a result of a contrast in acoustic impedances; an electromagnetic reflection occurs because of a contrast in electrical and dielectrical properties.
- subpolar glacier
- subpopulation
- sub-prime mortgage
- subprogram
- sub-pulse
- subrecursive hierarchy
- subring
- subroutine
- subsample
- subschema
- subscribe
- subscript
- subsemigroup
- subsequence
- subsequent stream
- subsequent streams
- subset
- subshell
- subsidence
- subsidiarity
- subsidiary
- subsidized credit
- subsidy
- subsistence
- subsistence farming