【增乘开方法】
拼译：evolution method of increasing multiplication
增乘开方法是中国数学家在宋元时期创造的一种开方和求高次方程数值解的方法，11世纪，由中国数学家贾宪首先创造，经12世纪的刘益，到13世纪秦九韶最后完成。19世纪，欧洲出现的霍纳法的步骤以及现代数学中综合除法的原理与它相同。据《九章算法纂类》记载，贾宪创造的增乘开方法，采用了随乘随加的方法得到减根方程。这种方法程序整齐，运算简捷，既可以直接推广到任意高次幂的开方，又可以运用到求高次方程的数值解。例如，求X=N的正根，设立方根有n+1位整数，先列开方式(1)，“实上商置第一位得数，以上商乘下法，置廉，乘廉为方，除实讫”，如(2)。其中商数10nX1以X1入算，如除尽，则10nX1就是所求根。否则，“复以上商乘下法
入廉，乘廉为方”，如(3)。“又乘下法入廉，其方一、廉二、下三退”，如(4)，(4)是减根方程(10nX1)3+3(10nX1)(10n－1X1)2+3·(10nX1)10n－1X1=N－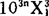
。再对(4)式重复上述步骤，直到求出所需要的答数。