A conic with eccentricity e=1. It is the locus of a point that moves so that its distance from the focus is equal to its perpendicular distance from the directrix. A chord through the focus, perpendicular to the axis, is called the latus rectum. For a parabola with its vertex at the origin, lying symmetrically about the x-axis, the equation is y2=4ax, where a is the distance from the vertex to the focus. The directrix is the line x=−a, and the latus rectum is 4a.
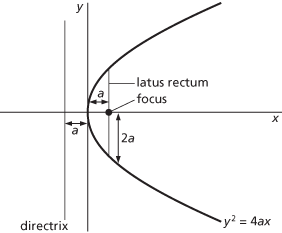
Parabola.
A conic with eccentricity equal to 1. Thus a parabola is the locus of all points P such that the distance from P to a fixed point F (the focus) is equal to the distance from P to a fixed line l (the directrix). It is obtained as a plane section of a cone in the case when the plane is parallel to a generator of the cone (see conic). A line through the focus perpendicular to the directrix is the axis of the parabola, and the point where the axis cuts the parabola is the vertex. It is possible to take the vertex as origin, the axis of the parabola as the x-axis and the focus as the point (a,0). In this coordinate system, the directrix has equation x =−a and the parabola has equation y2 =4ax (see normal form of conics).
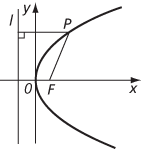
A parabola with focus and directrix
Different values of a give parabolas of different sizes, but all parabolas are the same shape (i.e. are similar to one another). The equations x = at2, y = 2at are parametric equations for the parabola y2 = 4ax.
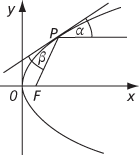
For a point P on the parabola, let α be the angle between the tangent at P and a line through P parallel to the axis of the parabola, and let β be the angle between the tangent at P and a line through P and the focus, as shown in the figure below;
A parabolic reflector
then α = β. This is the basis of the parabolic reflector: if a source of light is placed at the focus of a parabolic reflector, each ray of light is reflected parallel to the axis, so producing a parallel beam of light.
http://www.calculus.org/Contributions/animations.html Properties of the parabola with links to animated illustrations.
A type of curve whose ‘arms’ become parallel as they approach infinity, so that the curve never quite closes in on itself, defined mathematically as a conic section with an eccentricity of 1. It may be regarded as an ellipse in which the two foci are infinitely far apart, and is the limiting case between an ellipse and a hyperbola. Some comets have elliptical orbits that are so extended they are indistinguishable from parabolas.
- saturated compound
- saturated flow
- saturated(in networks)
- saturated mixing ratio lines
- saturated mode
- saturated model
- saturated solution
- saturated vapour pressure
- saturated velocity
- saturated zone overland flow
- saturation
- saturation current
- saturation deficit
- saturation magnetization and moment
- saturation moisture content
- saturation resistance
- saturation signal
- saturation spectroscopy
- saturation temperature
- saturation vapour pressure
- saturation voltage
- Saturn
- saturnian satellites
- Saturn Nebula
- Saturn rocket