A rank correlation coefficient that may be used as an alternative to Kendall’s tau. Individuals are arranged in order according to two different criteria (or by two different people). The null hypothesis is that the two orderings are independent of one another. It is based on the differences in the ranks given in two orderings. Suppose that the jth individual is given rank x_j in one ordering and rank y_j in the second ordering. Define d_j by d_j=x_j − y_j. Then ρ (which lies in the interval −1 to 1 inclusive) is given by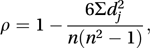where n is the number of individuals. In fact, ρ is the sample correlation coefficient for the pairs (x₁, y₁), (x₂, y₂),…, (x_n, y_n).

As an example, suppose that someone is asked to arrange, in order of increasing mass, five similar boxes whose contents vary. The correct order is 1, 2, 3, 4, 5, but the order chosen is 2, 1, 3, 5, 4. The rank differences are −1, 1, 0, −1, 1, giving Σd_j²=4. The value of ρ is 1 − (6 × 4)/(5 × 24)=0.8. Comparing this value with a table of critical values we find that, at the 5% significance level, there is no significant evidence to reject the null hypothesis that the boxes were arranged in a random order.