Theory relating the topology of a smooth surface (or more generally a manifold) with properties of smooth real functions on the surface, named after Marston Morse (1892–1977), who first published on the subject in 1925.

A Morse function on a smooth surface is a smooth real function with only non-degenerate stationary points (see Hessian), and so these are local maxima, local minima, or saddle points. For any smooth function f on a closed, smooth manifold X, it is the case that

where χ‎(X) denotes the Euler characteristic of X and #maxima denotes the number of maxima, etc. In the figure is a cross-section of a torus and f(x,y,z) = z is a Morse function on the torus. f has a maximum at D, a minimum at A, and saddle points at B and C. This correctly gives χ‎ = 1 − 2 + 1 = 0.

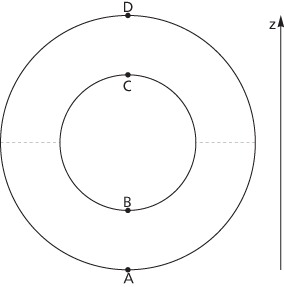
The height function on the torus

Morse theory includes results for the subsets of the surface of the form f ≤ k. In the figure, such a subset is that part of the torus below the dotted lines. For any z-coordinate k between B and C Morse theory states the subsets are homotopy equivalent. Further, the theory states how the homotopy type of the subset f ≤ k changes as k takes a stationary value.