The principal distribution used to model cyclic data; derived by von Mises in 1918. The distribution has two parameters: the circular mean μ, (− π<μ≤π), and κ (≥0), which is a measure of the concentration of the distribution.

If κ=0 then the distribution degenerates to the circular uniform distribution in which all directions are equally likely. As κ increases, the distribution becomes increasingly concentrated about μ. The probability density function f is given (with directions in radians) by 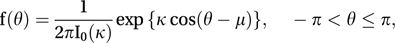where I₀(κ) is a modified Bessel function given by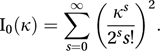The density function can either be pictured around a circle or it can be ‘unwrapped’ on to a line—in which case it resembles a normal distribution.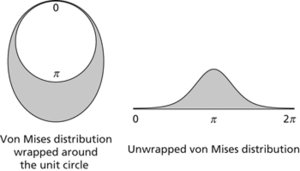

Von Mises distribution. The left diagram shows the density function wrapped around a central circle to give the continuous analogue of a rose diagram. The right diagram gives a more conventional representation but fails to emphasize that the right-hand edge joins the left-hand edge of the diagram. In either diagram the area of a portion of the shaded region is proportional to probability.