A theorem, proposed by Laplace, explaining the importance of the normal distribution in Statistics. Let X1, X2,…, Xn be independent random variables each having the same distribution, with mean μ and variance σ2. Let X̄, given by
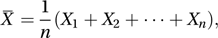 denote the sample mean. The central limit theorem states that, for large n, the distribution of X̄ is approximately a normal distribution with mean μ and variance ${1 \\over n}$σ2. Thus, for a large random sample of observations from a distribution with mean μ and variance σ2, the distribution of the sample mean is approximately normal with mean μ and variance ${1 \\over n}$σ2 and the distribution of the sample total is approximately normal with mean nμ and variance nσ2. The phrase ‘central limit theorem’ appears in the title (in German) of an article by Pólya published in 1920.
denote the sample mean. The central limit theorem states that, for large n, the distribution of X̄ is approximately a normal distribution with mean μ and variance ${1 \\over n}$σ2. Thus, for a large random sample of observations from a distribution with mean μ and variance σ2, the distribution of the sample mean is approximately normal with mean μ and variance ${1 \\over n}$σ2 and the distribution of the sample total is approximately normal with mean nμ and variance nσ2. The phrase ‘central limit theorem’ appears in the title (in German) of an article by Pólya published in 1920.
A statistical theorem which states that, in general, the probability distribution of the sum of a number of statistically independent random variables approximates to the Gaussian distribution as the number of variables becomes very large, irrespective of the distributions of the individual random variables. The central limit theorem is commonly used in the understanding and analysis of noise in communication systems.
In statistics, the theorem stating of a series of data sets drawn from any probability distribution, that the distribution of the means of those data sets will follow a normal distribution.
- oncogene
- oncogenic
- oncoid
- oncolite
- oncolith
- oncotic pressure
- one
- one-address instruction
- one-circle reflecting goniometer
- one-dimensional flow
- one gene–one polypeptide hypothesis
- one-level store
- one over many principle
- one-pass program
- one-place predicate
- one-plus-one address instruction
- one-port
- one-pot synthesis
- ONERA
- one-shot
- one-shot multivibrator
- one-sided abrupt junction
- one-sided confidence interval
- one-sided hypothesis
- Onesquethawian