An approximate value can be found for the definite integral
using the values of f(x) at equally spaced values of x between a and b. Divide the interval [a, b] into n equal subintervals of length h by the partition
where xi + 1 − xi = h = (b − a)/n. Denote f(xi) by fi, and let Pi be the point (xi, fi). If the line segment PiPi+1 is used as an approximation to the curve y = f(x) between xi and xi + 1, the area under that part of the curve is approximately the area of the trapezium shown in the figure, which equals . By adding up the areas of all the trapezia, the trapezium rule gives
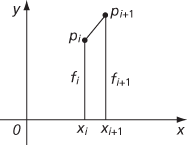
A single trapezium from the trapezium rule
as an approximation to the value of the integral. The error between this approximation and the definite integral is bounded above by
Simpson’s rule is significantly more accurate.
A method of finding an approximate value for an integral, based on finding the sum of the areas of trapezia. Suppose we wish to find an approximate value for . The interval a≤x≤b is divided up into n sub-intervals, each of length h=(b−a)/n, and the integral is approximated by
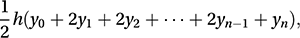
where yr=f(a+rh). This is the sum of the areas of the individual trapezia, one of which is shown in the diagram. The error in using the trapezium rule is approximately proportional to 1/n2, so that if the number of sub-intervals is doubled, the error is reduced by a factor of 4. A more accurate method for approximating an integral is Simpson’s rule.
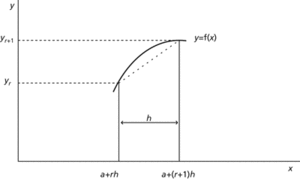
Trapezium rule. A method of approximate integration. A slight underestimate (as shown) will often be cancelled by a similar slight overestimate from another trapezium. Using narrower intervals will improve accuracy.
A form of numerical integration used to find the approximate area under a curve by dividing it into parts of trapezium-shaped sections that form columns of equal width with bases that lie on the horizontal axis. Also known as the trapezoidal rule, it is calculated from:
The approximation
used as the basis for an extrapolation method in numerical integration.
- entablature
- entailment
- entanglement
- entanglement entropy
- Entebbe raid (1976)
- entelechy
- entente cordiale (1904)
- enteric nervous system
- entering variable
- enterogastric reflex
- enterokinase
- enterolithic structure
- enteron
- Enterprise
- enterprise
- enterprise culture
- enterprise decision management
- Enterprise Investment Scheme
- enterprise modelling
- enterprise resource planning
- enterprise server
- enterprise system
- enterprise wiki
- enterprise zone
- enterprise zones