The electrical behaviour of transistors can be described more or less accurately by a number of equations relating the movement of the electrons in the semiconductor due to the applied potentials, and the resulting current flows. While this is useful for understanding transistor physics it is impractical for circuit design. Electrical models of the transistor behaviour have been devised that can be used in straightforward circuit analysis and design: these are equivalent circuit models, and the parameters of these models are the transistor parameters.

For circuit analysis by hand, the equivalent circuits are relatively simple. Generally they are divided into ‘DC’ models, for determining the steady bias conditions or operating point of the circuit, and small-signal models for determining the circuit response to an applied AC signal. Examples of such models for a bipolar junction transistor are the Ebers–Moll model, which is a DC model, and the hybrid-π model, which is a small-signal model (Figs. a, b). The transistor parameters in each model are the values for the equivalent-circuit components. For example, the parameters of the Ebers–Moll model are the current transfer ratios, α_F and α_R, and the saturation currents of the p-n junctions formed by the emitter-base and the collector-base junctions; the parameters of the hybrid-π model are the resistor and the capacitor values, and the transconductance.

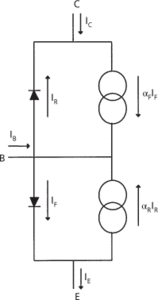
(a) Ebers–Moll DC model for a bipolar junction transistor

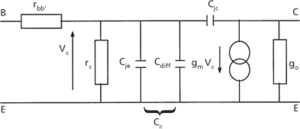
(b) Hybrid-π small-signal model for a bipolar transistor

Some small-signal models are derived from the two-port analysis of the transistor behaviour (see network). For example, the hybrid parameter model for a bipolar transistor in common-emitter configuration results in terms such as the input resistance h_ie, the output admittance h_oe, and the forward-current gain h_fe (gain parameter on the current-controlled current source at the output port). This hybrid parameter model is relatively archaic and should not be confused with the hybrid-π model of the bipolar transistor. The term h_fe is often found in transistor data sheets, and can be identified with the forward-current gain β.

In practical devices the equivalent-circuit models can also include components to model the packages that the devices are placed in. This is particularly important at high frequencies where the packages can contribute significant capacitance and inductance that can strongly affect the overall electrical behaviour of the transistor.

When computer-aided design is used in the circuit analysis and design, more sophisticated equivalent-circuit models can be employed, making use of the computational power available to perform many more calculations than would be possible by hand. The SPICE model for a bipolar transistor is shown in Fig. c, and the associated parameter list is given in the table. Various levels of sophistication can be included in such models.

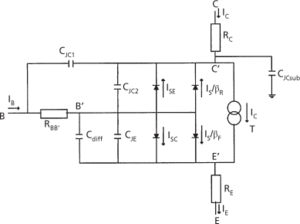
(c) SPICE model for bipolar transistor

Similar model approaches are employed for junction FETs and MOSFETs.