A test used in principal components analysis. The test is of the null hypothesis that the smallest m eigenvalues of a n×n variance–covariance matrix are equal to 0. Writing k=n−m+1, the test statistic is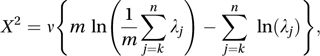where ν is the number of degrees of freedom associated with the variance–covariance matrix, and λ₁, λ₂,…, λ_n are the eigenvalues. Under the null hypothesis, X² has an approximate chi-squared distribution with (m−1)(m−2) degrees of freedom.