An experimental design that extends the randomized blocks design. In a Latin square two types of blocks are used. The numbers of both type of block must be equal to the numbers of treatments (m, say) being compared. The design is conveniently represented as an m×m square in which each experimental unit has been assigned to one treatment, one row, and one column in such a way that each treatment occurs exactly once in each row and exactly once in each column:

An extension of the Latin square introduces a fourth effect, represented by a Greek letter. The resulting design, in which each pair of letters occurs just once, with both the Greek letters and the Roman letters forming Latin squares, is called a Graeco-Latin square. Removal of a row or column from a Latin square results in a so-called Youden square (actually a rectangle). Youden squares can be used to generate balanced incomplete block designs.

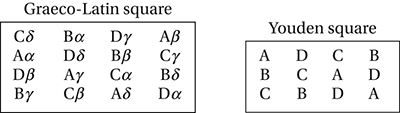
Latin squares were introduced into Statistics by Sir Ronald Fisher in 1925. Graeco-Latin squares were introduced by Fisher and Yates in 1934. In 1938 Fisher and Yates introduced Youden squares which they named after Youden.