Law for probabilities stating that if A and B are independent events then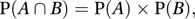and, in the case of n independent events, A₁, A₂,…, A_n,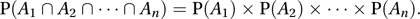

This is a special case of the more general law of compound probability, which holds for events that may not be independent. In the case of two events, A and B, this law states that

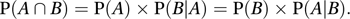
For three events, A, B, and C, this becomes

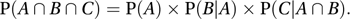
There are six (=3!) alternative right-hand sides, for example P(C)×P(A|C)×P(B|C ∩ A). The generalization to more than three events can be inferred. For definitions of symbols, see conditional probability; intersection.