A measure of the extent to which a set of observed frequencies (for example the numbers of plants in randomly distributed quadrats) follow a Poisson distribution. For a sample of n observations, let x̄ and s² denote, respectively, the sample mean and the sample variance (using the (n−1) divisor). Under the null hypothesis of a Poisson distribution the quantity I (the index of dispersion), given by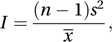has an approximate chi-squared distribution with (n−1) degrees of freedom. According to the null hypothesis the value of I should be near (n−1). This test is called the dispersion test.

If I is unusually large then the data are described as being over– dispersed, and, in the case of plants (or stars, or other point objects), the data are described as clustered. If I is unusually small then the data are described as displaying regularity. See extra-binomial variation.