A measure, h(t), of the chance that a component (or person), still working (or alive) at age t, is about to fail (or die). Formally, the hazard rate is defined by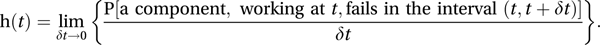The proportional-hazards model (also termed the Cox regression model) was proposed by Sir David Cox in 1972. It is a linear model in which the logarithm of the hazard rate, h(t), is related to one or more explanatory variables x₁, x₂, … as follows: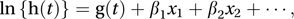where g(t) is an unspecified function of time and β₁, β₂, … are parameters.

The hazard ratio is the ratio of two hazard rates. If both hazard rates are described by the above model, with the same g function, then the hazard ratio is a function of the β-parameters of the two hazard rates.

The survivor function (also termed the survival function), S(t), is the probability that a component (or person) survives until time t. Thus

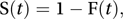
where F(t) is the lifetime cumulative distribution function.

The reliability function, which is the probability that the component is still working at time t, is an alternative description of the survivor function.

The hazard rate is related to the probability density function, f, and the survivor function by the equation

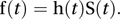
For many situations the graph of a hazard rate is a bathtub curve: initially the rate is high as the component beds in, there is then a constant hazard rate, and finally the component starts to wear out.

Hazard rate. The typical bathtub curve that results from a plot of the hazard rate against time. A high initial rate falls to a ‘normal level’ and then slowly increases as ageing sets in.

A plot of the survivor function against time is termed the survival curve. The survival time is the time until the occurrence of a particular event such as death or the failure of a component.