The product of a given number and all the whole numbers below it. It is usually written n!, e.g. factorial 4=4!=4×3×2×1=24. Factorial 0 is defined as 1.
For a positive integer n, the notation n! (read as ‘n factorial’ or ‘n shriek’) is used for the product n(n−1)(n−2)…×2×1. Thus 4!=4×3×2×1=24. Also, by definition, 0!=1. See also gamma function.
For a positive integer n, the ‘double factorial’ notation n!! denotes the products
If n is a positive integer, then factorial n, written as n!, is defined by
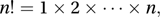with 0! defined to be 1. The notation was introduced in about 1810 by the French mathematician Christian Kramp (1760–1826). Factorial n is the number of different orderings of n individuals. The numerical value of n! increases rapidly with n: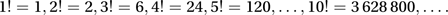
For n>1, successive values of n! can be calculated using
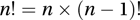If n is not an integer, factorial n can be defined via the gamma function Γ as
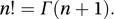For large values of n an approximation is provided by Stirling's formula.
The product of all the positive whole integers being considered. Note that 0! has a value of 1. For example, 5! is 0 × 1 × 2 × 3 × 4 × 5 = 20.