An estimate obtained by combining information from two or more independent samples taken from populations believed to have the same mean. Observations x11, x12,…, x1m are randomly selected from a population. Their mean is x̄1, given by
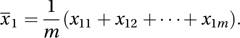 Random observations from a second population are denoted by x21, x22,…, x2n and have mean x̄2. If the two populations are believed to have the same mean, then a pooled estimate of the common mean is x̄, given by
Random observations from a second population are denoted by x21, x22,…, x2n and have mean x̄2. If the two populations are believed to have the same mean, then a pooled estimate of the common mean is x̄, given by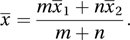 With k samples of sizes n1, n2,…, nk and with means x̄1, x̄2,… x̄k, the pooled estimate is given by
With k samples of sizes n1, n2,…, nk and with means x̄1, x̄2,… x̄k, the pooled estimate is given by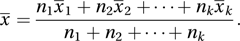 The unbiased estimate of the variance of the first population is , given by
The unbiased estimate of the variance of the first population is , given by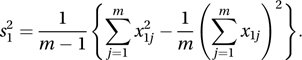 The corresponding estimate for the second population is . If it is believed that the two populations have the same variance, but possibly different means, then the pooled estimate of common variance is s2, given by
The corresponding estimate for the second population is . If it is believed that the two populations have the same variance, but possibly different means, then the pooled estimate of common variance is s2, given by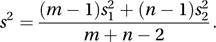 In the case of k samples, with the estimate from sample j being , the pooled estimate is given by
In the case of k samples, with the estimate from sample j being , the pooled estimate is given by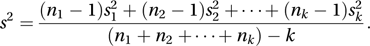 See also hypothesis test.
See also hypothesis test.
- Vitoria, Francisco de (c.1486–1546)
- VITOX process
- vitrage
- vitrain
- vitreous
- vitreous humour
- vitric horizon
- vitrification
- vitrinite
- vitroclastic
- monadic
- monadic operation
- monadnock
- Monadology
- monalphabetic
- monarchy
- Monasteries, Dissolution of the (1536–40)
- monastery
- monatomic molecule
- monazite
- monchiquite
- Monck, George, 1st Duke of Albemarle (1608–70)
- MOND
- Mondex
- Mond, Ludwig (1838–1909)