【宇宙距离尺度】
拼译：cosmic distance scale
天体的距离是天文学中最重要的一个参数。只有知道了天体的距离，才可能揭示和了解该天体的本原和真象。太阳和月球投影在天球上的角直径都是30角分左右，看上去差不多大小。日地平均距离约是地月距离的400倍，所以太阳的直径实际比月球的大400倍。天体的距离测量不仅直接涉及对恒星的了解，也影响到对银河系的大小、河外星系的本原以及可观测宇宙的规模的认识。离我们最近的恒星的视差是0．772角秒(折合成长度是4．2光年)，也就是说除太阳之外，所有的恒星的视差均小于1角秒。现代地面天文三角视差测量的精度最高是0．01～0．02角秒，因此，有效的测量的空间范围是50～100pc(约合150～300光年)。银河系的圆盘结构的直径约是25kpc(约8万光年)，距离的直接测量只局限于太阳附近的很小空间。自从1838年利用三角视差法测出第1个恒星的距离以来，在150年间，经几代天文学家的努力，已取得三角视差测量值的恒星总数还不超过一万个，这和银河系成员恒星总数约为1000～2000亿个相比，仅是极小的一部分。所以，尽管恒星距离测量的基础是三角视差，但更多更远的天体的距离资料出自非直接的测量方法。
天文学中习惯地将视差和距离视为同义语，凡用间接方法取得的恒星距离也被称为视差。根据移动星团(例如毕星团)在天球上投影的几何方法取得的星团距离称为星群视差；利用食变星的轨道运动称为力学视差；用赫罗图主星序拟合法求出的距离叫测光视差；利用同一光谱型的巨星和矮星的谱线差异测定的距离叫分光视差；根据恒星自行测定的距离称为平均视差；藉助天体光谱中叠加的星际谱线测定的距离叫星际视差；等等。在宇宙距离测量领域遵循的原则有两条：一是同类者相同，二是远近者相同。前一条说的是同一类天体，具有同样的或相近的天体物理特征。例如，凡是太阳型恒星均有和太阳相同或相近的质量、光度、化学丰度、年龄等等；凡是天琴RR型变星均有和天琴RR相似的质量、平均光度、光变特征等等。后一条指的是宇宙内的物质和物质的表现、分布等特征，无论在近处的，还是在远处的均相同，在过去的和现在的也相同。例如，银河系内的发光物质的主要表现形式是恒星，其它星系中也如此；银河系附近的各种宇宙物质的丰度分布和遥远空间内的一样。有了这两个前提，才能建立起宇宙距离测量的基本手段，即由近及远的阶梯法。首先测出太阳附近空间内的各种类型天体的距离，然后在遥远空间证认出同种类型天体，比较二者的亮度等观测数据，按距离和亮度成反比的基本定则求出远处天体的距离。银河系内天体距离的测定 除了上述的三角视差法和其他间接测量法之外，在银河系内最佳的可作为指示距离的标准烛光是天琴RR型变星和造父变星。1895年，美国贝利(S．I．Bailey)在几十个球状星团中发现了1885个变光天体，其光变周期多在0．2～1．0d之间。在同一星团内，这些变星无论其周期长短，平均亮度一致，差异不超过0．1星等。1899年，美国弗莱明(W．Fleming)发现并确认一个脉动变星天琴RR。1908年，她证认出贝利发现的球状星团变星是和天琴RR为同类天体，遂称为天琴RR型变星。1914年，美国沙普利(H．Shapley)利用自行法，求出天琴RR型变星的平均光度为0．0星等，这是天文学史上第1个做为标准烛光的天体。沙普利利用天琴RR型变星测量出凡拥有这类变星的球状星团的距离，并根据球状星团的空间分布求出银河系的规模大小。将天琴RR型变星的平均光度定为0．0星等，意味着确定了距离的尺度。若尺度定得比客观实际值大些，则用该指示距离的天体测定的距离值比实际值近些；反之，尺度小些，则比实际值远些。1991年，欧南天文台的天文小组发现天琴RR型变星的平均光度与金属丰度有关。金属丰度少者，光度大。新求出的平均光度是0．20～0．38星等，比以前公认的的0．0星等要暗些，即距离尺度更大些。用这个新测定的尺度，求出的天体距离值比以前用平均光度为0．0星等的尺度测出的距离值近10%～20%。造父变星也是一种最佳的指示距离的标准烛光。1908年，美国莱维特(H．S．Leavitt)分析她在小麦哲伦云中发现的25个造父变星的观测资料。它们的光变周期最短的1．25d．最高的127d。莱维持发现，造父变星的光变周期和亮度呈线性关系，即光变周期越长者，亮度越大。因为这25个造父变量都是小麦哲伦云中的成员，可以认为它们和观测者之间的距离都是相等的。所以，亮度大小反映的就是光度大小。后世称之为造父变星的周光关系。1913年，丹麦赫茨普龙(E．Hertzsprung)根据银河系中的13个造父变星的自行，求平均视差，确定了周光关系中的光度零点。赫茨普龙以造父变星的周光关系作为标准烛光，求出小麦哲伦云的距离，发现它原来是银河系之外的河外星系。对银河系外天体距离的测定 由于造父变星为高光度天体，在4Mpc(约1200万光年)的距离上，仍可得见。因此，可以用周光关系作为距离指示物去计量银河系附近凡能观测到造父变星的星系的距离。问题的关键是距离尺度的定标。1918年，沙普利认为造父变星周光关系的暗端(即周期短到1．0d的一端)的光度和天琴RR型变星的平均光度相同，从而为周光关系确定了零点，使之成为测量凡可见造父变星的近距星系的距离的标准烛光。从此，这个被公认的距离尺度一直沿用了30多年。1952年，旅美德国天文学家巴德(W．Baade)证明，虽然造父变星和天琴RR型变星都是脉动变星，但属于不同的星族。二者的光度没有天体物理上的联系，光变周期最短的造父变星的平均光度不是0．0星等，而是－1．5星等，即光度应是0．0星等的4倍。这样，距离尺度应缩短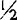
。用这个新定标的距离尺度去度量河外星系，求出的距离值比以前的值远上一倍。星系的直径也相应的要加上一倍。将作为标准烛光的造父变星去标定更高光度的天体的平均光度，例如，星系中的最亮星的亮度、行星状星云的角直径、电离氢区的角大小、超新星的极大光度，等等，从而将距离的测量范围阶梯式地扩大到宇宙深处。由于造父变星的周光关系是从银河系内过渡到银河系外的标准烛光，所以，使这一距离尺度更准确反映宇宙真实面貌始终是现代天文学的重要课题。宇宙距离尺度的建立和订正 对于比30Mpc(约1亿光年)更遥远的河外天体而言，现有的由近及远的阶梯法不能精确地测定其距离。1929年，美国哈勃(E．P．Hubble)根据前人于1912～1926年期间测定的46个星系的视向速度以及他本人测定的这些星系的距离，发现星系的退行速度和距离成正比，即V=HD，式中V是km／s表示的退行速度，D是以Mxpc为单位的星系距离，H是比例常数。后人将此经验关系式称为哈勃定律，将H称为哈勃常数。V值是观测值，在确定了H值后，即可将哈勃定律作为距离指示物，求出星系的距离D。H值的测定基础仍是恒星的三角视差、天琴RR型星的平均光度、造父变星的周光关系等一系列由近及远的标准烛光。1929年，哈勃常数H值测定为500km／s．Mpc。60多年来，历经几代天文学家订正，今日使用的H值有两个，其一是50km／x．Mpc，另一是100km／x．Mpc。前者为一较小的距离尺度，用之测出的距离远；后者，尺度较大，测出的距离近。二者相差一倍。也就是说，用小尺度求出的可观测宇宙要更深远一倍。1990年，美国用航天飞机放送哈勃空间望远镜(HST)上天。这个口径2．4m的反射望远镜的一项主要任务是研究星系中的距离指示天体，从而更精确地求出哈勃常数H，以期用改善的距离尺度描述我们周围的宇宙。【参考文献】：1 Hodge P W. Annual Review of Astronomy & Astrophysics, 1981,19:3572 Rowan-Robinson M. Cosmological distance ladder,19853 Van den Bergh S,et al. Extragalactic distance scale, 19884 Clementini G,et al. The absolute magnitrde of RR Lyrae stars, Messenger, 1991,65:275 Madore B, et al. Cepheid distance scale, Publications of Astromical Society of the Pacific,1991,103:933(北京天文台博士生导师李竞研究员撰)