“向量值最优化问题的对偶性”的概念、定义、翻译、参考文献-科学参考

单词

向量值最优化问题的对偶性

释义

【向量值最优化问题的对偶性】

拼译：on duality for vector valued optimizatoin problems

向量值最优化也叫多目标最优化或多目标规划。20世纪40年代后期线性规划中完美的对偶理论和50年代初Kuhn、Tucker的里程碑式的论文，鼓励很多学者把对偶性的概念推广到非线性规划以至更一般的规划问题，60年代二次规划、凸规划对偶理论的成功创立，将对偶理论的研究推向一个新的高潮，使之成为数学规划的重要组成部分，70年代向量值最优化蓬勃发展以来，其对偶理论的研究也占有极其重要的地位，并取得了可喜的进展。

称一对向量值最优化问题(一个叫原问题，另一个叫对偶问题)关于某种含义的最优解是对偶的，通常指它们满足下述条件：(1)其中一个是极小化(min)问题，另一个是极大化(max)问题。(2)极小化问题的任一可行解的相应目标函数值不小于极大化问题的任一可行解的相应目标函数值。(3)若一个问题有某种意义下的最优解，则另一个问题也有同一意义下的最优解，且相应的目标函数值相等。

对偶理论的主要问题是：建立对偶模型(给定原问题，建立合适的对偶问题)，在适当条件下证明上述(2)、(3)成立。

早在1951年，线性规划诞生初期，D．Gale、H．W．Kuhn和A．W．Tucker就建立了矩阵最优化(包含向量线性最优化为特殊情况)的对偶模型，归结为向量线性规划即为

其中A∈R^m×n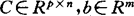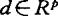，，，x∈Rⁿ，u∈R^m，。

Gale等人证明了上述规划关于有效解的对偶性。

1974年，J．S．H．Kornbluth提出了如下向量值线性最优化对偶模型：

其中A∈R^m×n，C∈R^p×n，B∈R^mxp，λ∈R^p，x∈Rⁿ，u∈R^m，μ∈R^p。

他证明这一对向量值线性规划关于有效解(真有效解)的对偶性并用之于灵敏度分析。

1977年，W．Rödder提出向量(矩阵)值函数的鞍点概念，并将Gale等人的对偶理论纳入其中，还给出了(VLP_GKT)与(VLP_K)、(VLD_GKT)与(VLD_K)的解之间的关系。

1978年，H．Isermann证明了如下多目标线性规划的对偶性：

1983年，J．W．Nieuwenhuis利用择一定理，给出了这一对规划的对偶性一个简单的证明。

1985年，E．H．Ivanov和R．Nehse讨论了以上各对向量值线性规划对偶模型之间的关系，Y．Sawaragi等人在锥序下建立了以上各对向量线性规划对偶模型关于非控解的对偶理论。

向量值非线性最优化的对偶理论，近年来讨论较多、影响较大的有Lagrange型对偶、Wolfe型对偶、Mond-Weir型对偶、共轭型对偶。这些都是标量最优化已有对偶模型的推广，其对偶定理的证明也基本上是借助标量最优化来完成的，但其中的难度也不小。

设有向量值非线性最优化问题(原问题)：

其中，f(x)、g(x)和h(x)分别是p维、m维和k维向量值函数。

1979年，T．Tanino和Y．Sawaragi对上述原规划定义了向量值Lagrange函数：

L(x，u，v)=f(x)+《u^Tg(x)+v^Th(x)》

其中《u^Tg(x)+v^Th(x)》表示各个分量均为u^Tg(x)+v^Th(x)的p维向量函数。通过引入两个集值映射：原映射和对偶映射，将标量凸规划的Lagrange对偶理论推广到向量值最优化，这是一项极有价值和影响的杰出成果。

1981～1988年，林锉云研究了(VP)的Wolfe型对偶问题：

他先后在多种广义凸性条件下，证明了关于(弱)有效解的对偶性。1987年，R．R．Egudo和M．A．Hanson在不变凸性条件下，证明了(VP)和(VD)关于Geoffrion真有效解的对偶性。

1980～1985年，B．D．Craven、G．Bitran、B．D．Corley、E．H．Ivanov和R．Nehse将上述Lagrange函数中的向量u和v分别用矩阵A和B代替，给出了新的Lagrange函数：

L(y，A，B)=f(y)+Ag(y)+Bh(y)，A∈R^p×m，B∈R^p×k提出了类似上述(VD)的对偶规划，并在(VP)为凸规划的情况下，证明了关于有效解的对偶性。

1988年，刘三阳对一类非光滑非凸向量值最优化证明了Wolfe型对偶性。

1981年，B．Mond和T．Weir提出了新颖的最优化对偶模型，对上述向量值最优化(VP)而言，其对偶问题为

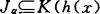其中的分量下标集)，的分量下标集)，α=0，1，…，r，某些I_α或J_α可以是空集，，。

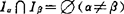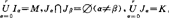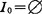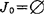特别当I₀=M，J₀=K时，(VD_Mw)变为前面的Wolfe型对偶模型，当

，

，I₁=M，J₁=K时，(VD_MW)变为如下形式：

这个对偶模型有一个显著特点，就是与原问题(VP)具有相同的目标函数，很多文献中所说的Mond-Weir型对偶往往是指这个模型。

Mond-Weir对偶模型提出以来，很受重视，1986年以来，WeiI、Egudo、Mond、Craven和Hanson等人分别在各种条件下(包括伪凸性，拟凸性和不变凸性)，研究了Mond-Weir型对偶理论，刘三阳在非光滑非凸情况下，分别研究了(VP)和(VD_Mw)及(VD_MW)的对偶性。

共轭对偶理论是利用共轭函数来建立对偶模型的。相应于原问题(VP)引进扰动函数

及其共轭函数

φ^*(T，A，B)=max｛Tx+Au+Bv－φ(x，u，v)｜x∈Rⁿ，

，v∈R^k｝其中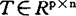

，A∈R^p×m，B∈R^p×k，φ^*是集值映射。

1980年，Tanino和Sawaragi给出的共轭对偶模型为

(VP_TS) minφ(x，0，0)(VD_TS) max－φ^*(0，A，B)

(VP_Ts)与(VP)等价，在凸性条件下，他们证明了(VP)与(VD_Ts)关于有效解的对偶性，1981～1982年，H．Kawasaki用不同的方式研究了共轭对偶模型关于弱有效解的对偶性，1981年，S．Brumelle用“inf”和“sup”分别代替“min”和“max”，证明了共轭对偶模型关于真有效解是对偶的，1984年，汪寿阳在非控解意义下建立了向量值最优化的共轭对偶理论，1992年，周厚春、程钧谟在有效解意义下推广了集值映射的共轭函数定义，给出了向量最优化的广义共轭对偶理论。

也有不通过扰动函数研究共轭对偶性的，J．Zown和C．Gros分别在1975年和1978年推广了Fenchel的共轭对偶理论，对凸向量值最优化建立了与上面对偶模型截然不同的共轭对偶形式和对偶定理。

此外，向量值最优化的对称对偶和自身对偶理论也取得一定进展，1983～1989年，林锉云、Weir、Mond和Hanson等人在这方面作了很有价值的工作。

值得一提的是，在中国，林锉云对向量值最优化对偶理论研究得最早，成就最为突出。

关于向量值最优化的对偶理论，目前还不完善，需要研究的问题还很多，特别值得提出的是：(1)建立新的对偶模型。(2)发展和完善共轭对偶理论。(3)深入系统研究集值分析，对向量值最优化问题中遇到的集值映射作重点探讨，这有可能发展成为向量值最优化的重要理论基础。(4)研究非光滑、非凸最优化问题的对偶性。(5)对偶性与最优性、稳定性和计算方法的互相结合与渗透。．

【参考文献】：

1 Isermann H．Zeit Oper，Res，1978，22：33～41

2 Gros C．European J Oper Res，1978，2：368～376

3 林锉云．高等学校计算数学学报，1981，3(1)：18～25

4 林锉云．应用数学学报，1983，6(1)：76～85

5 汪寿阳．系统科学与数学，1984，4(4)：303～313

6 Sawaragi Y" Nakayama H,Tanino T. Theory of multiobjec-tive optimization, New York:Academic press,Inc, 1985

7 Egudo R R, Hanson M A. J. Math. Anal. Appl 1987,126: 469～477

8 Weir T . J Austral Math Soc(Series A) ,1987,43:21～34

(西安电子科技大学博士生导师刘三阳撰；游兆永审)

随便看

科学参考收录了7804条科技类词条，基本涵盖了常见科技类参考文献及英语词汇的翻译，是科学学习和研究的有利工具。