【联合逼近】
拼译：simultaneous approximation
由单点逼近发展到联合逼近最初是由f及导数f′同时逼近引起，然后C，Lp等空间有限个或一列函数F=｛Fn｝被逼近，有sup联合与∑联合两大类，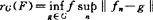
、
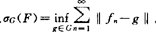。每种又有弱形，比如
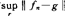换为
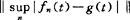。20世纪60～70年代顺利解决了F=｛f1，f2｝或有限个情形，化为单个函数被逼近为主，如J．Diaz、Mclaughlin、G．Phillips、Sahney、Holland、史应光、王美琴、王建忠、徐士英、McGabe、W．Ling等人均有建树。例如Ling解决了
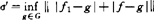化为单点逼近
，指出当
，则σ′=2e，且联合佳逼元(b．s，a．)唯一，当
则σ′=‖f2－f1‖，非唯一。
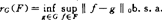元g0的全体记ZG(F)。特别G是全空间，记为r(F)，Z(F)，即F的车贝半径与车贝中心集。联系1962年Garkavi的首创工作，b．s．a．的存在性与唯一性研究者颇多。F设为紧集或一般有界集区别很大。T．Narang1983引用F对G可远距性是介乎中间的F条件。获知(Rx)∩(R)空间中，F紧，G闭凸，则b．s．a．唯一存在。1976年E．Rozemap．Smith由一个引理推出当F对G可远距，G是自反子空间，则b．s．a．唯一存在。X自反，G闭凸，F有界则推b．s．a．存在。X严凸，G凸，F对G可远距则推b．s．a．唯一。潘文熙已引入一种强化近紧性(叫工类近紧)，是指对任何相对于G可远距的F，当
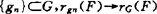则存在子gni→g∈G。他证实(Rx)∩(H)空间中G闭凸，则G是工类近紧的。当G工类近紧，F对G，可远距，则b．s．a．存在。1979年J．Mach研究存在性时创立一崭新概念：(X，G)具(P1)性(G是X中闭子集)，乃指
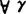＞0，ε＞0，
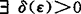及h(x，y)，x，y，h∈G，‖h－x‖＜ε，当｜θ｜＜δ则
。若h(x．y)连续时，叫(P2)性。(P1)性保证对凡有界集F，b．s．a．存在，(P2)对ZG(F)映射连续性起作用，1980年Mach再度引入(Q1)，(Q2)性(按他原作叫P1，P2性实，与前者不能混同)是对(G，B)，B是某些有界集F之类而言，1991年A．Chiacchio和J．Prolla引入(G，B)具(A)性概念，亦保证b．s．a．存在，特别B是任何单点集之类时，转化为Yost性。(A)性对研究Cb(S．G)中b．s．a．有重要作用。对于b．s．a．的本性及属性，单点逼近的著名Kolmogorov条件移植到紧集F情形联逼是成立的。而使用了极大泛函集
这里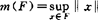
。潘国权、郭元明都指出由K．氏条件必要性需要引出联合太阳集概念产生，它比单点逼近的太阳集严格，但比凸性弱。郭氏证明严凸空间中对F紧，G是联合太阳集，则b．s．a．只≤1个，此外引入范数“于F处”弱导数
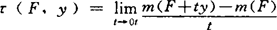，则为b．s．a．又一本征条件乃τ(F－g0，g0－g)≥0，这里F紧，G凸。又一本征乃任g∈G，
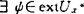及x∈F有ψ(x－g)≥ψx－g0≥rg0(F)(Amir－Mach判别法)。特别当G是n维子空间，又化为
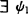，…ψn∈extSF－g0及x0，…，xn∈F，
，使ψi(xi－y0)=rg0(F)，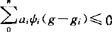
，
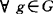。对ZG(F)集的性质，1984年Amir－Mach指出F可“割弃”一个球B(g0，t)，0≤t≤rg0(F)以替F不影响g0佳逼性。而G也可适当割弃或扩伸，像单点逼近那样。关于ZG(F)、Z(F)集的分布，1964年Garkavi指出希氏空间则任有界集F，Z(F)∩
，且反之推空间此性。1976年Rozema得任闭子空间G，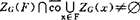
亦表征希氏空间，而且G改用闭凸集却不真。比如选G为球体，F是球外的两点可验知。映射F1→ZG(F)自Mach记作CentG：2x→2G，叫联合度量投影，或叫车贝中心映射。1978年指出X匀凸，则映射单值存在且一致连续。C(S，X)中亦如此。1980年Amir和Ziegler则减弱设X相对于G匀凸亦成立。A．P．Bosznay1978获知(Rx)∩(LUR)空间中，闭子空间G，则centG单值存在且连续。潘文熙获得度量空间中，若G有某种强近紧性，F0有界，F0的某Hausdorff度量领域的任意F都使ZG(F)为单点时，则centG于F0处连续。这推广了著名的Singer定理，从而一定条件空间中，G闭凸，F对G可远距便可CentG连续。潘氏进一步研究(UR)中CentG，连续性获量性公式，找到了局部连续模。设G闭凸F，F′有界(b．s．a．Z，Z′就存在唯一)则
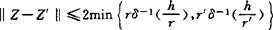，这里h=h(F，F′)，r=rG(F′)。特别在希氏空间呈
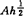形，Mach的Q1，Q2性对centGu．s．c．性等有重要用途。潘氏再考虑了G变动时的连续性G1→ZG(F)，它也是Lip的，且只要h(G，G1)／r＜2则
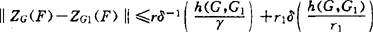。这里X匀凸，G闭凸，r1=rG1(F)。其他情形右边改成Ah(G，G1)形，他同时考虑了Gn↓（∞时‖ZGn(F)－ZG∞(F)‖→0的问题。对CentG连续模必将更深化研究。猜想当CentG具一定的收缩Lip性会导致X是内积空间这一类Hirschfeld型命题迟早会发现。CentG的连续选问题也必然将开展研究。联合强唯一性已初步有研究。潘－郭开始考虑m(F－g)－m(F－g0)≥μ‖g－g0‖，
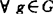，这时g0叫联合强佳逼元(s．b．s．a．)，μ叫强唯一常数。若F紧G闭凸，已证明sup｛Ref(g0－g)：f∈extSF－g0｝≥K‖g－g0‖导致g0是s．b．s．a．找到此式的种种等价条件，这推广了单点逼近时P．F．Mah(1984)所讨论的各条件。又μ=μ(F)有一种u．s．c．性
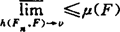。联合拟强唯一性mp(F－g)－mp(F－g0)≥μp‖g－g0‖p。人们注意到Smarzewski(1986，1988)就单点逼近对Lp(μ)已有完善结果。当p≥2求得
郭元明对联合逼近分别G闭凸集，闭子空间时获得
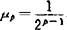与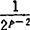
，结果相当完美。求联合佳逼点概念可扩张到求最佳N网，军事上为布置炮台群问题
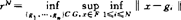，达到左方那个inf的｛
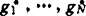｝叫最佳N网。N=1回复b．s．a．这是1962Garkavi最早引入的。他指出G紧，或者共轭B空间中G是W*闭集，则凡有界集F，最佳N网存在。当G是子空间，涉及G* *到G有范数1投影性等也保证存在性。潘文熙剖析γN=0的条件及深入讨论最佳N网存在性。对两集最近距离
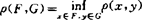，潘氏系统讨论最近点对ρ(x0，y0)=ρ(F，G)存在性及唯一性，以及近渡点x0，P(x0，F)=P(F，G)性质及叠映射PFPG的不动点有关性质。关于最近点对存在性1988年XuXiubin获一些充分条件：F紧弱，G凸，G关于F可近，则最近点对存在。潘氏获另一些充分条件：(1)F紧，G关于F可近，或(2)F闭囿紧，G关于F可近，且有界，(3)自反，F，G皆弱闭，一个有界。最近点对唯一性方面，引入严凸集，x，
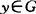，0＜θ＜1，则θx+(1－θ)y∈intG起了重要作用。潘氏还建立仿射集、超平面、直线种种之间最近距离的命题，又涉及许多带距离性分离定理，大大推进了Mazur的结果，开拓了泛函逼近论的新篇章。【参考文献】：1 Ling W H. Pro AMS, 1975,48:185～1882 Maeh J.M Ann,1979,24,157～1643 Narang TD. JAT,1983,39:93～964 Amir D. JAT,1984,40:364～3745 Mah P F. JAT,1984,41:91 ～996 潘文熙、郭元明．全国第5届逼近论会议论文集．河南大学学报(增刊)．1988(暨南大学潘文熙教授撰)