【渐近鞅理论】
拼译:theory of asymptotic martingales
自20世纪50年代经典鞅论完成后,近代鞅论迅猛发展的同时,人们考虑能否减弱鞅定义中的条件而仍能保持鞅的部分性质,其主要特点是鞅条件在各种不同的极限意义下成立,这就是自60年代开始发展起来的渐近鞅理论。设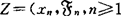 是实值适应可积序列,
是实值适应可积序列,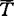 和T分别表示(
和T分别表示(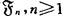 )停时和有界停时全体,记T(σ)={τ∈T:τ≥σ},
)停时和有界停时全体,记T(σ)={τ∈T:τ≥σ},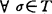 。
。
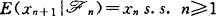 ;②称Z是拟鞅(Quasimartingale),若
;②称Z是拟鞅(Quasimartingale),若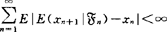 ;③称Z是渐近鞅(Amart),若
;③称Z是渐近鞅(Amart),若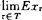 存在且有限;④称Z是依概渐近鞅(Pramart),若
存在且有限;④称Z是依概渐近鞅(Pramart),若





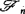 ,n≥1)使有
,n≥1)使有 且在An上有
且在An上有 ;⑾称Z是终鞅(EM),若
;⑾称Z是终鞅(EM),若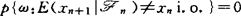 ;⑿称Z是拟终鞅(QEM),若
;⑿称Z是拟终鞅(QEM),若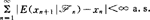 ;⒀称Z是L1-极限鞅(1)(L1-Mil(1)),若
;⒀称Z是L1-极限鞅(1)(L1-Mil(1)),若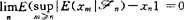 ;⒁称Z是L1-极限鞅(2)(L1-Mil(2)),若
;⒁称Z是L1-极限鞅(2)(L1-Mil(2)),若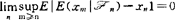 .上述序列也称为鞅型序列,它们之间有下述关系:
.上述序列也称为鞅型序列,它们之间有下述关系:
若把上述序列定义中的绝对值|·|改为[·]+(-),就得到相应的上(下)鞅型序列。例如称Z是极限下鞅(3),若
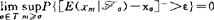 ,
,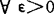 ,对给定的σ域流(
,对给定的σ域流(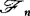 ,n≥1),设
,n≥1),设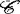 表示具有某一特性的实值(
表示具有某一特性的实值( ,n≥1)适应的可积序列全体,称
,n≥1)适应的可积序列全体,称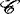 具有:(A)可选停止性,若对每一个
具有:(A)可选停止性,若对每一个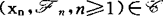 ,有
,有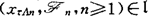 ,
,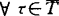 (B)可选采样性,若对每一个
(B)可选采样性,若对每一个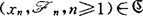 ,对任取的上升停时列
,对任取的上升停时列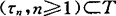 ,均有
,均有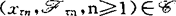 。(C)Riesz分解性,若对每一个(xn,Fn,n≥1)∈1,有分解xn=Mn+zn,n≥1
。(C)Riesz分解性,若对每一个(xn,Fn,n≥1)∈1,有分解xn=Mn+zn,n≥1其中(Mn,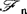 ,n≥1)是鞅,而EznIA→0,n→∞,
,n≥1)是鞅,而EznIA→0,n→∞,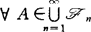 ;
;
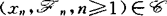 ,
,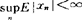 有
有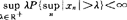 ;(E)a.s.收敛性,若对每一个
;(E)a.s.收敛性,若对每一个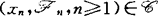 ,
,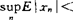 ∞,
∞,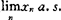 存在;(F)变换性,若对每一个
存在;(F)变换性,若对每一个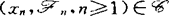 ,(un,
,(un,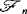 ,n≥1)可料序列(i)若(un,n≥1)一致有界,则
,n≥1)可料序列(i)若(un,n≥1)一致有界,则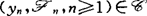 ,其中
,其中
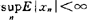 ,在集合
,在集合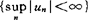 上
上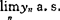 存在(G)差方可加性,若对每一个
存在(G)差方可加性,若对每一个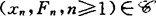 ,
,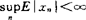 ,有
,有
表1

说明:(1)表中√表示有此性质,×表示无此性质,×*表示在条件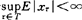 下有此性质。
下有此性质。
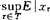 |<∞下有变换性(ii)。关于鞅型序列及其有关性质的一系列结果,常称为渐近鞅理论,几乎与此同时,向量值渐近鞅理论也被建立。设(
|<∞下有变换性(ii)。关于鞅型序列及其有关性质的一系列结果,常称为渐近鞅理论,几乎与此同时,向量值渐近鞅理论也被建立。设(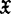 ,‖·‖)是一Banach空间,
,‖·‖)是一Banach空间,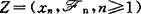 是
是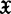 值Bochner可积适应序列,若把实值鞅型序列定义中的绝对值|·|换成‖·‖,即可得到相应的向量值鞅型序列的定义。例如称Z是一致渐近鞅,若
值Bochner可积适应序列,若把实值鞅型序列定义中的绝对值|·|换成‖·‖,即可得到相应的向量值鞅型序列的定义。例如称Z是一致渐近鞅,若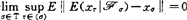 。当
。当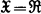 时,渐近鞅与一致渐近鞅是等价的,但在一般Banach空间中,只有一致渐近鞅
时,渐近鞅与一致渐近鞅是等价的,但在一般Banach空间中,只有一致渐近鞅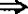 渐近鞅成立。向量值鞅与鞅型序列的鞅性质常与值空间
渐近鞅成立。向量值鞅与鞅型序列的鞅性质常与值空间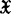 的几何性质有关。例如,1985年M.Talagrand证明了下述命题——设
的几何性质有关。例如,1985年M.Talagrand证明了下述命题——设 是一Banach空间,则下述等价:(1)
是一Banach空间,则下述等价:(1)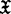 有RNP,(2)满足条件
有RNP,(2)满足条件 的任一
的任一 值Mil(3)必a.s.按范数拓扑收敛。现在,实值与向量值渐近鞅理论已趋于成熟,随着随机集理论的兴起,集值鞅与渐近鞅理论正处于发展阶段。【参考文献】:1 Edgar G A, et al. J, Multivariate Anal,1976,6:193~221, 572~5912 Millet A, et al. Can J Math, 1980,32:86~1253 Gut A, et al. L.N. M, 1983,10424 Egghe L. Stopping time techniques for analysts and proba-bilists. Cambridge University Press, 19845 TomkinsRJ. Can J Statist,1984,12:99~1066 Talagrand M. Ann of Probability , 1985,13:1192 ~1203
值Mil(3)必a.s.按范数拓扑收敛。现在,实值与向量值渐近鞅理论已趋于成熟,随着随机集理论的兴起,集值鞅与渐近鞅理论正处于发展阶段。【参考文献】:1 Edgar G A, et al. J, Multivariate Anal,1976,6:193~221, 572~5912 Millet A, et al. Can J Math, 1980,32:86~1253 Gut A, et al. L.N. M, 1983,10424 Egghe L. Stopping time techniques for analysts and proba-bilists. Cambridge University Press, 19845 TomkinsRJ. Can J Statist,1984,12:99~1066 Talagrand M. Ann of Probability , 1985,13:1192 ~1203(华东师范大学汪振鹏教授撰)