【混料试验设计】
拼译:mixture experimental design
是安排混料试验和分析混料数据的数学理论和方法。合理地选择少量的试验点,通过不同的百分比试验得到指标与各成分比例之间的回归方程,从而得到最优配方。
混料试验设计的研究是联系开发性工作的应用基础的研究,其研究成果具有很好经济效益和广泛的社会效益。在工业试验方面,已在润滑油、火药、汽油混合物、混凝土、聚合物塑料、合金、陶瓷、油漆、食品、制药、磨具磨料、混纺纤维和烧结矿等产品的研究研制中得到应用。在理论上,它的研究涉及到许多数学分支,例如,组合数学、代数拓扑学、N维几何学、泛函分析、突变理论等。它的研究也提出许多新的数学问题有待解决。混料试验设计自20世纪60年代开始发展之际就是试验设计的一个重要分支。美国H.Scheffè于50年代末60年代初发表的一系列论文为混料试验设计的发展奠定了基础。由于混料试验设计具有明显的实际应用价值,所以它引起了许多数理统计学家和实际工作者的研究兴趣,发表了许多学术论文,其中以美国和原苏联学者的论文较多,1981年美国John Wiley and Sons出版公司出版的美国J.A.Cornell所著《Experiment with Mixtures》是世界上第1本关于混料试验设计的专著,书中较全面地论述了到出版时为止关于混料试验设计的研究成果。假定用y表示试验指标,用x1,x2,…,xq表示q分量系统中各分量所占的百分比,混料试验设计是要在混料约束条件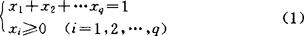
的限制下合理地选择试验点,得到y关于xi(i=1,2,…,q)的回归方程,使得计算简单、分析容易和回归方程精度好,便于推测最适宜的混料配方。由于混料约束条件(1)的限制,使得混料试验所采用的回归模型不同于一般常用的回归模型。混料试验设计中最基本、最常用的回归模型是Scheffè混料规范多项式和多重线性多项式。例如,q分量二阶Scheffè混料规范多项式为

0≤ai≤xi≤bi≤1(i=1,2,…,q) (3)
这里,ai和bi(i=1,2,…,q)都是由具体问题决定的常数。关于有上、下界约束的混料问题,可以采用极端顶点设计、XVERT算法设计、剖分设计等方法来解决。
由于混料问题的约束条件(1)的限制.混料数据的分析方法也不同于一般回归分析中常用的数据分析法,而是使用混料数据分析法。例如,为通过回归方程预测指标的极大(小)值,我们不能简单地通过求回归方程的一阶导数且令其为零来得到,而要求条件极值。为了适应不同的混料问题,人们也给了许多不同于多项式的其它类型的混料模型,例如,附加倒数项的多项式模型、Becker的齐次模型、对数比模型、可加模型和比率模型等。传统的混料问题,假定指标不受混料总量的影响,但在一些问题中,混料总量也要影响指标。例如,对某农作物施以混合肥料,不仅各种肥料在总量中的百分比(分量比例),而且总的施肥量(总量)也影响指标(产量)。如何给出简单实用而且易于解释的含有总量因子的混料回归模型及其试验点尽量少的试验设计,此问题虽有一些结果,但有些问题还有待于研究。对于同时含有“成分变量”及“过程变量”的混料问题,传统的解决办法是采用这两类变量的“乘积模型”及其“乘积设计”。“乘积设计”的缺点是试验点太多难于实施。实践证明:多数情况下,两类因子间的(高阶)乘积项不存在(或可以忽视)。如何给出简单实用的简化了的两类变量的“乘积模型”及其试验点较少而且性能良好的设计,这将是混料试验设计的一个研究热点,即所谓的“析因混料试验设计”,它将是人们关注的一个重要目标。最优设计和混料设计,是试验设计学科的两个分支,科学发展要求将它们结合起来。最优混料设计将是人们关注的研究热点。对于各种混料模型,分别研究各种最优标准下的最优设计,可以期待得到一批研究结果。使用混料设计,要比使用正交设计和析因设计等复杂。特别是实际中常遇到的分量具有上、下界附加约束,或者分量的线性组合具有上、下界附加约束的混料试验,其试验设计和数据分析更为复杂。研制适于微型机用的混料设计的算法及其应用软件是混料试验设计的一个应用课题。【参考文献】:1 Wiley and Sons, 19812 Steinberg DM, et al. Technometrics,1984,26:71 ~ 1303 Atkinson A C. International Statistical Review, 1988,56(2):99~1154 Dodge Y , et al. Optimal Design and Analysis of Experi-ments. North-Holland, 19885 关颖男.混料试验设计.上海:上海科学技术出版社,1990(东北大学关颖男教授撰)