【最佳腾起角】
拼译:the optimum takeoff angle
利用质点抛射理论,探求跳远运动(投掷运动)初速度V0的最佳方向,即最佳腾起角(最佳投掷角)αopt,以提高运动成绩。这个问题的研究早已开始,然而并未得到解决。 沿袭至今的最佳腾起角计算公式,是将V0与α看成2个独立变量,然后通过位移对α微分求极值而得到的。1981年海(J.G.Hay)据此对优秀跳远运动员的最佳腾起角作了计算(表1)。计算表明,优秀运动员在43°左右腾空最佳,而实践反复表明以20°左右腾起为宜。与此类似,滑步推铅球最佳投掷角理论值在42°左右,而实际以37°左右投掷为宜。理论与实践的不一致性,尚存在争议。表1
一些学者认为理论计算是对的,故实际采用的角度是保守的。1974年宋春华提出,努力加大腾起角,特别是在板前速度高度发挥的现在,已经成了跳远中的关键。1982年李建英提出急行跳远腾起角不应小于40°。1987年吴忠贯认为腾起角在43°最佳,并指出,不敢把腾起角加大,恐惧水平速度损失,是跳远的实践与理论研究中普遍存在着的错误观点。另外一些学者立足于客观实践,坚持20°左右腾起为好。1977年戴森(G.Dyson)指出,45°可以获得最大抛射距离而被人皆知,并有时被推荐,但这样要求是错误的,实际采用的最大角度应比45°小得多。1978年埃克(T.Aech)提出,人们所希望的45°腾起角很难做到,实际的角度相当低,超过25°的腾起角几乎没有。他指出跳远中不要大肆夸张垂直方向的速度,保持前进速度,正确踏板才是重要的。1987年捷列兹(T.Gelles)指出大多数优秀运动员的腾起角都不超过25°,运动员起跳动作越快腾起角就越小。1980年程国庆认为,由于运动员的水平速度和垂直速度的某些差异,腾起角一般应当在25°~35°之间。1985年卡洛金(М.П.Калакин)等提出起跳角在75°~80°,腾起角在16°~25°为合适。1990年葛隆祺的研究表明,沿袭至今的公式只适用于原地跳远(原地投掷),对于急行跳远(滑步投掷),V0与α已成为描述合运动的物理量,它们互为相关,因此原有求极值的处理方法是错误的,所得公式也不正确。真正独立变量有3个:即牵连速度V1、相对速度V2和它们之间的夹角θ,通过位移对θ微分求极值才能找到最佳起跳角(θopt)和最佳腾起角。数值计算表明(表2),世界优秀运动员最佳腾起角理论值在20°左右,推铅球最佳投掷角在37°左右,理论与实践相符。葛隆祺所给的最佳角度近似计算公式(Δh=0),简明扼要,可供教学与训练参考。表2 θopt与αopt的关系 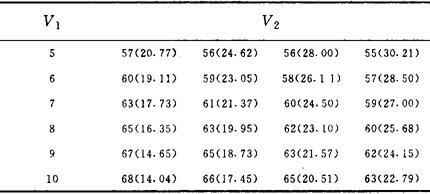
注:计算时取Δh=0.6m。速度:m/s,角度:度;括号中为αopt最佳腾起角的研究还有许多工作要做:(1)最佳角度θopt、αopt不仅依赖于V1和V2,还与重心降低幅度Δh有一定关系,希望能得出由V1、V2和Δh计算最佳角度的精确公式。(2)制订由V1、V2和Δh查找最佳角度的曲线图表,供体育训练用。(3)改进现有测量技术,力求快速准确测出瞬时速度V1和V2以及角θ和α,以便通过图表对比检验运动动作技术是否合理,并提出修改方案。(4)现行教科书和文献中沿袭已久的最佳角度计算公式要作适当更正。【参考文献】:1 宋春华.体育技术资料.国家体科所编.1974.112 Dyson G.The Mechanics of Athletics,Holmes & Meier Publishers.Inc.,19773 程国庆.运动生物力学.北京:人民体育出版社,1980,1994 Hay J G.The Biomechanics of Sports Techniques,19815 李建英.上海体院学报,19826 Калакин М П.Леткая Xрестоматия Издателbcтво,Физкуль-тyра И Спорт,Мoсква,19857 吴忠贯.浙江体育科学,1987,2:85~878 葛隆祺.力学与实践,1990,12(6):51~539 葛隆祺.广州:华南理工大学出版社,1990,591~593(浙江师范大学葛隆祺副教授撰) |

