The geometrical definition of the centroid G of a triangle ABC is as the point at which the medians of the triangle are concurrent. It is, in fact, ‘two-thirds of the way down each median’, so that, for example, if A’ is the midpoint of BC, then AG = 2GA’. This is the point at which a triangular lamina of uniform density has its centre of mass. It is also the centre of mass of three particles of equal mass situated at the vertices of the triangle.

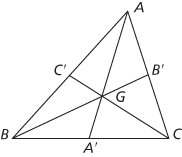
The centroid G of ABC

If A, B, and C have position vectors a, b, and c, then G has position vector $\frac{1}{3}(a+b+c)$.